题目内容
4. 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,将△ABC折叠,使点B恰好落
如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′=3.
分析 设EB′=x,根据勾股定理求出AC的长,根据翻折变换的性质用x表示出EC、EB′、CB′,根据勾股定理列出方程,解方程即可.
解答 解:设EB′=x,
∵∠B=90°,AB=6,BC=8,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
由折叠的性质可知,BE=EB′=x,AB′=AB=6,
则CB′=AC-AB′=4,EC=BC-BE=8-x,
由勾股定理得,x2+42=(8-x)2,
解得x=3,
∴EB′=3.
故答案为:3.
点评 本题考查的是翻折变换的性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界是1.
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界是1.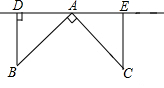 如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.
如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.
 把14个棱长为1的正方体,在地面上堆叠成如图所示的立体,然后将露出的表面部分染成红色,那么红色部分的面积为33.
把14个棱长为1的正方体,在地面上堆叠成如图所示的立体,然后将露出的表面部分染成红色,那么红色部分的面积为33.