题目内容
4.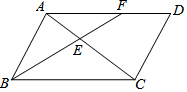 如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.
如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.(1)求证:AB=AF;
(2)当AB=6,BC=10时,求$\frac{AE}{AC}$的值.
分析 (1)由在?ABCD中,AD∥BC,利用平行线的性质,可求得∠FBC=∠AFB,又由BF是∠ABC的平分线,易证得∠ABF=∠AFB,利用等角对等边的知识,即可证得AB=AF;
(2)易证得△AEF∽△CEB,利用相似三角形的对应边成比例,即可求得$\frac{AE}{AC}$的值.
解答 (1)证明:∵BF平分∠ABC,
∴∠CBF=∠AFB,
∴∠ABF=∠CBF,
∴∠ABF=∠AFB,
∵平行四边形ABCD,
∴AB=AF,
∴∠ABF=∠CBF,
∴∠ABF=∠AFB,
∵平行四边形ABCD,
∴AB=AF,
(2)解:∵AB=6,
∴AF=6,
∵AF∥BC,
∴△AEF∽△CEB,
∴$\frac{AF}{BC}$=$\frac{AF}{BC}$=$\frac{6}{10}$=$\frac{3}{5}$,
∴$\frac{AE}{AC}=\frac{3}{8}$.
点评 此题考查了相似三角形的判定与性质、平行线的性质以及等腰三角形的判定.此题难度不大,注意数形结合思想的应用,注意有平行线与角平分线易得等腰三角形.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
15.用直接开平方的方法解方程(2x-1)2=x2做法正确的是( )
| A. | 2x-1=x | B. | 2x-1=-x | C. | 2x-1=±x | D. | 2x-1=±x2 |
19.平面直角坐标系中,△ABC关于y轴的对称图形是△A'B'C',若BC边上有点P(a,b),则它的对应点P'的坐标为( )
| A. | (a,b) | B. | (a,-b) | C. | (-a,b) | D. | (-a,-b) |
9.已知$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}ax+by=11\\ ax-by=-3\end{array}\right.$的解,则a+b的算术平方根为( )
| A. | ±3 | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
16. 若数a、b、c在数轴上的位置如图所示,则|a|-|a-c|+|b+c|的化简结果为( )
若数a、b、c在数轴上的位置如图所示,则|a|-|a-c|+|b+c|的化简结果为( )
 若数a、b、c在数轴上的位置如图所示,则|a|-|a-c|+|b+c|的化简结果为( )
若数a、b、c在数轴上的位置如图所示,则|a|-|a-c|+|b+c|的化简结果为( )| A. | -2a+b+2c | B. | c | C. | -b-2c | D. | b |
13.下列四个变形过程中错误的是( )
| A. | 若$\frac{4}{5}$($\frac{5}{4}$x-10)=8,则x-8=8 | B. | 若1-$\frac{1-x}{5}$=x,则5-1+X=5x | ||
| C. | 若-$\frac{1}{2}$(3x+6)+4x=1,则-$\frac{3}{2}$x+3+4x=1 | D. | 若3x-5y=-3,则-5y+3=-3x |
14.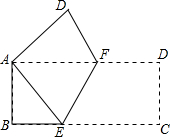 如图,将AB=4,BC=8的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长是( )
如图,将AB=4,BC=8的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长是( )
 如图,将AB=4,BC=8的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长是( )
如图,将AB=4,BC=8的矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
 如图在△ABC中,∠B=∠C,∠ADE=∠AED,∠EDC=20°,则∠BAD的度数为40度.
如图在△ABC中,∠B=∠C,∠ADE=∠AED,∠EDC=20°,则∠BAD的度数为40度.