题目内容
20.在平面直角坐标系中,有一点B(a,b)的横纵坐标满足条件:|2a-24|+(a-b-7)2=0.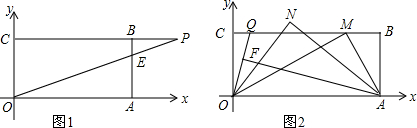
(1)求点B的坐标.
(2)如图1,过点B作BA⊥x轴于A,BC⊥y轴于C,P为CB延长线上一点,OP交BA于E,若S△OAE-S△BPE=18,求P、E两点坐标.
(3)M为(2)中BC上一点,如图2,且OM⊥AM,Q为CM上一动点,F为OQ上一动点,∠FAO=∠COQ,ON、AN分别平分∠QOM与∠FAM,当Q点运动时,∠N变化吗?若不变,求其值;若变化,说明理由.
分析 (1)根据非负数的性质得2a-24=0,a-b-7=0,解方程组求出a和b即可得到点B的坐标;
(2)设P(m,5),E(12,n),根据平行线分线段成比例得$\frac{m-12}{12}$=$\frac{5-n}{n}$,解得n=$\frac{60}{m}$,则E(12,$\frac{60}{m}$),再利用三角形面积公式得到$\frac{1}{2}$•12•$\frac{60}{m}$-$\frac{1}{2}$•(5-$\frac{60}{m}$)•(m-12)=18,解得m=$\frac{84}{5}$,则n=$\frac{25}{7}$,所以P($\frac{84}{5}$,5),E(12,$\frac{25}{7}$);
(3)如图2,由∠FAO=∠COQ可得∠AOF+∠AOF=90°,则∠AFO=90°,根据三角形内角和可得∠QOM=∠MAF,再利用角平分线定义得∠NOM=$\frac{1}{2}$∠QOM,∠MAN=$\frac{1}{2}$∠MAF,所以∠NOM=∠MAN,然后再利用三角形内角和易得∠N=∠AMO=90°.
解答 解:(1)∵|2a-24|+(a-b-7)2=0,
∴2a-24=0,a-b-7=0,
∴a=12,b=5,
∴点B的坐标为(12,5);
(2)设P(m,5),E(12,n),则PB=m-12,BE=5-n,
∵PB∥OA,
∴$\frac{PB}{OA}$=$\frac{BE}{AE}$,即$\frac{m-12}{12}$=$\frac{5-n}{n}$,
∴n=$\frac{60}{m}$,
∴E(12,$\frac{60}{m}$),
∵S△OAE-S△BPE=18,
∴$\frac{1}{2}$•12•$\frac{60}{m}$-$\frac{1}{2}$•(5-$\frac{60}{m}$)•(m-12)=18,解得m=$\frac{84}{5}$,
∴n=$\frac{25}{7}$,
∴P($\frac{84}{5}$,5),E(12,$\frac{25}{7}$);
(3)∠N不变化.
如图2,
∵∠FAO=∠COQ,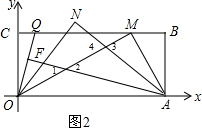 ∠AOF+∠COQ=90°,
∠AOF+∠COQ=90°,
∴∠AOF+∠AOF=90°,
∴∠AFO=90°,
∵∠AMO=90°,∠1=∠2,
∴∠QOM=∠MAF,
∵ON、AN分别平分∠QOM与∠FAM,
∴∠NOM=$\frac{1}{2}$∠QOM,∠MAN=$\frac{1}{2}$∠MAF,
∴∠NOM=∠MAN,
∵∠3=∠4,
∴∠N=∠AMO=90°,
即∠N不变化.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了非负数的性质、三角形内角和定理和三角形面积公式.

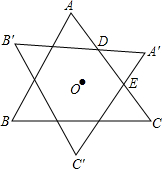 如图,将等边三角形ABC绕其外心O顺时针旋转α(0°<α<120°)至△A′B′C′,交AC于点D,E,若以AD,DE,EC为三边所围成的三角形为直角三角形,则旋转角α=30°或90°.
如图,将等边三角形ABC绕其外心O顺时针旋转α(0°<α<120°)至△A′B′C′,交AC于点D,E,若以AD,DE,EC为三边所围成的三角形为直角三角形,则旋转角α=30°或90°.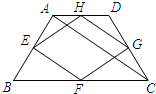 如图,某农场有一块四边形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线AC=BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )
如图,某农场有一块四边形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线AC=BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )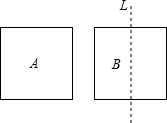 操作:有2张边长都是2的正方形纸片A和B,请你将纸片A的一边的一个端点放在纸片B的对称轴L上,另一个端点与纸片B的一个顶点重合后压平.求纸片A与纸片B重合部分的面积.
操作:有2张边长都是2的正方形纸片A和B,请你将纸片A的一边的一个端点放在纸片B的对称轴L上,另一个端点与纸片B的一个顶点重合后压平.求纸片A与纸片B重合部分的面积.