题目内容
18.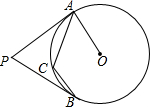 如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )| A. | 140° | B. | 145° | C. | 110° | D. | 125° |
分析 连结OA、OB,∠ADB为弧AB所对的圆周角,如图,根据切线的性质得∠OAP=∠OBP=90°,再利用四边形内角和可计算出∠AOB=110°,接着根据圆周角定理得到∠D=$\frac{1}{2}$∠AOB=55°,然后根据圆内接四边形的性质计算∠ACB的度数.
解答 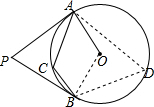 解:连结OB,∠ADB为弧AB所对的圆周角,如图
解:连结OB,∠ADB为弧AB所对的圆周角,如图
∵PA,PB分别与⊙O相切于A,B两点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°-70°=110°,
∴∠D=$\frac{1}{2}$∠AOB=55°,
∴∠ACB=180°-∠D=125°.
故选D.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.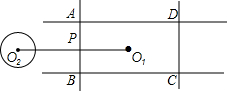 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )| A. | 18次 | B. | 12次 | C. | 8次 | D. | 4次 |
9.若菱形的周长为24cm,一个内角为60°,则菱形较短的一条对角线为( )
| A. | 9cm | B. | 8cm | C. | 7cm | D. | 6cm |
6. 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 3 | D. | 无法确定 |
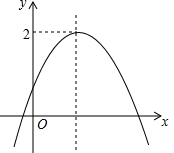 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其顶点的纵坐标是2,有下列结论: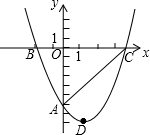 如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.
如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点.