题目内容
8.不等式组$\left\{\begin{array}{l}{-2x-2<0}\\{\frac{x}{2}+1≥x}\end{array}\right.$的解集是-1<x≤2.分析 先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集.
解答 解:$\left\{\begin{array}{l}{-2x-2<0…①}\\{\frac{x}{2}+1≥x…②}\end{array}\right.$,
解①得:x>-1,
解②得:x≤2.
则不等式组的解集是:-1<x≤2.
故答案是:-1<x≤2.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.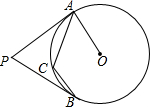 如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
 如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )| A. | 140° | B. | 145° | C. | 110° | D. | 125° |
3.某音乐会的门票价格如表,小明用2800元做为预定门票的资金
(1)若全部资金用来预定B等级、C等级门票共8张,问B等级和C等级门票各订多少张?
(2)小明想用全部资金预定指定A等级门票、B等级和C等级门票共12张,他的想法能实现吗?若不能,请说明理由;若可以,请求出各种类型门票的张数.
| 等级 | 票价(元/张) |
| A | 150 |
| B | 300 |
| C | 500 |
(2)小明想用全部资金预定指定A等级门票、B等级和C等级门票共12张,他的想法能实现吗?若不能,请说明理由;若可以,请求出各种类型门票的张数.
13.下列运算正确的是( )
| A. | a2+a3=a5 | B. | a3•a2=a6 | C. | a0=1 | D. | 2015-1=-$\frac{1}{2015}$ |
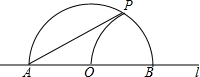 如图,直线l上一点O,以O为圆心,任意长为半径画半圆,交l于A、B两点,再以B为圆心,OB的长为半径画弧交半圆于P,连AP,则sin∠PAB的值等于$\frac{1}{2}$.
如图,直线l上一点O,以O为圆心,任意长为半径画半圆,交l于A、B两点,再以B为圆心,OB的长为半径画弧交半圆于P,连AP,则sin∠PAB的值等于$\frac{1}{2}$.
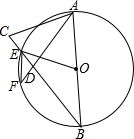 如图,等腰三角形ABC中,BA=BC,以AB为直径作圆,交BC于点E,圆心为O.在EB上截取ED=EC,连接AD并延长,交⊙O于点F,连接OE、EF.
如图,等腰三角形ABC中,BA=BC,以AB为直径作圆,交BC于点E,圆心为O.在EB上截取ED=EC,连接AD并延长,交⊙O于点F,连接OE、EF.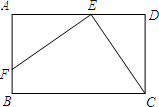 如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,则AE的长为6cm.
如图,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm,矩形ABCD的周长为32cm,则AE的长为6cm.