题目内容
9.若菱形的周长为24cm,一个内角为60°,则菱形较短的一条对角线为( )| A. | 9cm | B. | 8cm | C. | 7cm | D. | 6cm |
分析 由菱形的性质得出AB=AD=6cm,由已知条件∠BAD=60°,证出△ABD是等边三角形,得出BD=AB即可.
解答 解:如图所示:
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∵菱形ABCD的周长为24cm,
∴AB=AD=6cm,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=6cm,
故选:D.
点评 本题考查了菱形的性质、等边三角形的判定与性质;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
20.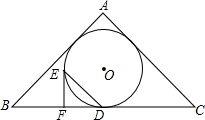 如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
 如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
17.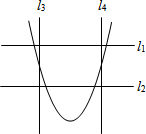 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )| A. | l1为x轴,l3为y轴 | B. | l1为x轴,l4为y轴 | C. | l2为x轴,l3为y轴 | D. | l2为x轴,l4为y轴 |
18.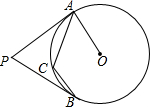 如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
 如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )| A. | 140° | B. | 145° | C. | 110° | D. | 125° |
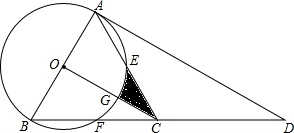 如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F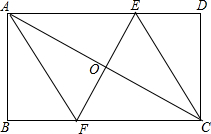 如图,已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,连接AF、CE.
如图,已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,连接AF、CE.