��Ŀ����
����һ������ˮ���Ļ����ν��ڼ䣬����ͬѧ����һ�������ǰȥ���Σ�����������Ϊ180Ԫ������ʱ������������ͬѧ�����ÿ��ͬѧ��ԭ����̯��3ԪǮ���ѣ���μ�������ͬѧ��x�ˣ�Ӧ������г����̣���������⣬ֻ�г����ɣ�
 ����������������ԭ���μ�������ͬѧ��x�ˣ�����������Ϊ180Ԫ������ʱ������������ͬѧ�����ÿ��ͬѧ��ԭ����̯��3ԪǮ���ѣ����з��̣�
�����������μ�������ͬѧ��x�ˣ���ô����ǰΪx��2�ˣ�
����������Եó�
����������������ԭ���μ�������ͬѧ��x�ˣ�����������Ϊ180Ԫ������ʱ������������ͬѧ�����ÿ��ͬѧ��ԭ����̯��3ԪǮ���ѣ����з��̣�
�����������μ�������ͬѧ��x�ˣ���ô����ǰΪx��2�ˣ�
����������Եó�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д���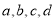 ����
����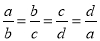 ,��
,��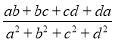 ��ֵΪ�� ��
��ֵΪ�� ��
A. 1��0 B. 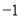 ��0 C. 1��
��0 C. 1��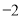 D. 1��
D. 1��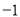
 D
����������,�� �� ����a+b+c+d ʱ����k=1����a+b+c+d=0ʱ��k=-1�� .
��ѡD.
D
����������,�� �� ����a+b+c+d ʱ����k=1����a+b+c+d=0ʱ��k=-1�� .
��ѡD. ijѧУ��420ԪǮ���̳�ȥ����84������Һ���������ۣ�ÿƿ����0.5Ԫ���������ԭ�۶�����20ƿ����ԭ��ÿƿ����Ԫ������ԭ��ÿƿ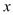 Ԫ������г�����Ϊ�� ��
Ԫ������г�����Ϊ�� ��
A. 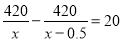 B.
B. 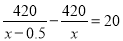
C. 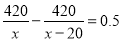 D.
D. 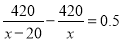
 B
����������ԭ��ÿƿxԪ������ijУ��420ԪǮ���̳�ȥ����84������Һ���������ۣ�ÿƿ����0.5Ԫ���������ԭ�۶�����20ƿ�����з��̣�
��������
��ԭ��ÿƿxԪ��
=20��
��ѡB��
B
����������ԭ��ÿƿxԪ������ijУ��420ԪǮ���̳�ȥ����84������Һ���������ۣ�ÿƿ����0.5Ԫ���������ԭ�۶�����20ƿ�����з��̣�
��������
��ԭ��ÿƿxԪ��
=20��
��ѡB�� ��ͼ��ijС����һ��ƽ���ı��εĻ�̳���ֱ����к졢�ơ������̡��ȡ���6����ɫ�Ļ��������AB��EF��DC��BC��GH��AD����ô����˵��������ǣ� ��
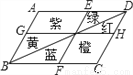
A. �컨���̻���ֲ���һ����� B. �ϻ����Ȼ���ֲ���һ�����
C. �컨��������ֲ���һ����� D. �������ƻ���ֲ���һ�����
 C
����������AB��EF��DC��BC��GH��AD��
��GH��BD��EF��һ��ƽ���ı��ηָ���ĸ�Сƽ���ı��Σ�
��һ���Խ��߿���һ��ƽ���ı��ε����һ��Ϊ����
�ݴ˿ɴ�ͼ�л��S��=S����S��=S�죬S����+��+�̣�=S����+��+������
���ݵ������ԭ��֪S��=S�ȣ�
��A��B��D˵����ȷ��
�ٿ���S����S����Ȼ����ȣ�
��ѡC��
C
����������AB��EF��DC��BC��GH��AD��
��GH��BD��EF��һ��ƽ���ı��ηָ���ĸ�Сƽ���ı��Σ�
��һ���Խ��߿���һ��ƽ���ı��ε����һ��Ϊ����
�ݴ˿ɴ�ͼ�л��S��=S����S��=S�죬S����+��+�̣�=S����+��+������
���ݵ������ԭ��֪S��=S�ȣ�
��A��B��D˵����ȷ��
�ٿ���S����S����Ȼ����ȣ�
��ѡC�� ��ͼ��ƽ���ı���ABCD�ĶԽ��߽��ڵ�O����AB=5����OCD���ܳ�Ϊ23����ƽ���ı���ABCD�������Խ��ߵĺ��ǣ� ��
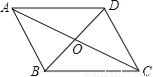
A. 18 B. 28 C. 36 D. 46
 C
�������������������ƽ���ı��ε����ʺ���֪�������㼴�ɣ�����ע����ƽ���ı���ABCD�������Խ��ߵĺ�ʱҪ�������Խ��߿���һ�����壮
��������
���ı���ABCD��ƽ���ı��Σ�
��AB=CD=5��
�ߡ�OCD���ܳ�Ϊ23��
��OD+OC=23��5=18��
��BD=2DO��AC=2OC��
��ƽ���ı���ABCD�������Խ��ߵĺ�=BD+AC=2��DO+OC��=...
C
�������������������ƽ���ı��ε����ʺ���֪�������㼴�ɣ�����ע����ƽ���ı���ABCD�������Խ��ߵĺ�ʱҪ�������Խ��߿���һ�����壮
��������
���ı���ABCD��ƽ���ı��Σ�
��AB=CD=5��
�ߡ�OCD���ܳ�Ϊ23��
��OD+OC=23��5=18��
��BD=2DO��AC=2OC��
��ƽ���ı���ABCD�������Խ��ߵĺ�=BD+AC=2��DO+OC��=... ���ʽ����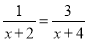 �Ľ���________
�Ľ���________
 -1
������������ͬʱ�����ĸ��x+2��(x+4)��������ʽ����Ϊ��x+4=3x+6�����x=-1���������Ƿ��̵Ľ�,�ʴ�Ϊ��x=-1.
-1
������������ͬʱ�����ĸ��x+2��(x+4)��������ʽ����Ϊ��x+4=3x+6�����x=-1���������Ƿ��̵Ľ�,�ʴ�Ϊ��x=-1. ����ʽ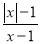 ��ֵΪ0����x��ֵ����___________
��ֵΪ0����x��ֵ����___________
 -1
�������������������Ϊ��ʱ��ʽ��ֵΪ�㣬����ң�����x=1��
-1
�������������������Ϊ��ʱ��ʽ��ֵΪ�㣬����ң�����x=1�� ��x2��6x��9��|y��2|��Ϊ�෴������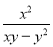 ��
��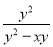 ��ֵΪ__.
��ֵΪ__.
 ����������x2��6x��9��|y��2|��Ϊ�෴����
��x2��6x��9+|y��2|=0��
��(x-3)2+|y��2|=0��
��x+3=0,y-2=0,
��x=3,y=2,
�࣫
=
=
=
=
=
=.
����������x2��6x��9��|y��2|��Ϊ�෴����
��x2��6x��9+|y��2|=0��
��(x-3)2+|y��2|=0��
��x+3=0,y-2=0,
��x=3,y=2,
�࣫
=
=
=
=
=
=. ��ͼ���ڵ�����ABC�У�AB=AC��BD��AC����ABC=72�㣬���ABD=�� ��
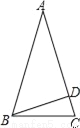
A. 36�� B. 54�� C. 18�� D. 64��
 B
��������������������ݵ��������ε���������֪����á�A=36�㣬�ٸ��ݴ�ֱ�Ķ�����������ڽǺͶ���������á�ABD=90�㩁36��=54�㣮
��ѡ��B��
B
��������������������ݵ��������ε���������֪����á�A=36�㣬�ٸ��ݴ�ֱ�Ķ�����������ڽǺͶ���������á�ABD=90�㩁36��=54�㣮
��ѡ��B�� 
