题目内容
6．
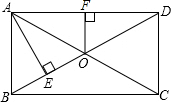如图，矩形ABCD中，对角线AC、BD相交于点O，AE⊥BO于E，OF⊥AD于F，已知OF=3cm，且BE：ED=1：3，求BD的长．
分析 由矩形的性质和已知条件证出OF是△ABD的中位线，得出AB=2OF=6cm，再由线段垂直平分线的性质得出OA=AB=6cm，即可得出BD的长．
解答 解：∵四边形ABCD是矩形，
∴OA=OC=$\frac{1}{2}$AC，OB=OD=$\frac{1}{2}$BD，
∴OA=OB=OD，OF⊥AD，
∴AF=DF，
∴OF是△ABD的中位线，
∴AB=2OF=6cm，
∵BE：ED=1：3，
∴OE=BE，
∵AE⊥BO，
∴OA=AB=6cm，
∴BD=2OB=2OA=12cm．
点评 本题考查了正方形的性质、三角形中位线定理、线段垂直平分线的性质；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
16．A、B两个水果市场各有荔枝13吨，现从A、B向甲、乙两地运送荔枝，其中甲地需要荔枝14吨，乙地需要荔枝12吨，从A到甲地的运费为50元/吨，到乙地的运费为30元/吨，从B到甲地的运费为60元/吨，到乙地的运费为45元/吨．
（1）设A地到甲地运送荔枝x吨，请完成下表：
（2）设总运费为W元，请写出W与x的函数关系式，并直接写出x的取值范围．
（3）怎样调送荔枝才能使运费最少？
（1）设A地到甲地运送荔枝x吨，请完成下表：
| 调往甲地（单位：吨） | 调往乙地（单位：吨） | |
| A | x | 13-x |
| B | 14-x | x-1 |
（3）怎样调送荔枝才能使运费最少？
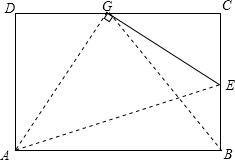如图，矩形纸片ABCD的边AB=10cm，BC=6cm，E为BC上一点，将矩形纸片沿AE折叠，点B恰好落在CD边上的点G处，求BE的长．
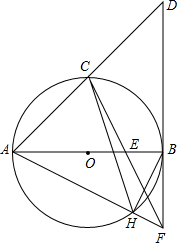如图，AB是⊙O的直径，点C是$\widehat{AB}$的中点，⊙O的切线BD交AC的延长线于点D，E是OB的中点，CE的延长线交切线BD于点F，AF交⊙O于点H，连接BH．