题目内容
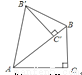
如图，把Rt△ABC绕点A逆时针旋转40°，得到Rt△AB′C′，点C′恰好落在边AB上，连接BB′，则∠BB′C′=________度．
20°
【解析】试题分析：根据旋转图形可得∠B′AB=40°，AB=AB′，则∠B′BA=70°，根据∠BCB′=90°可得∠BB′C=90°－70°=20°.
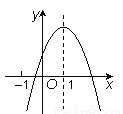
阅读快车系列答案二次函数y＝ax2＋bx＋c的图象如图11所示，且P＝|2a＋b|＋|3b－2c|，Q＝|2a－b|－|3b＋2c|，则P，Q的大小关系是______．
P＞Q
【解析】∵抛物线的开口向下，
∴a＜0，
∵
∴b＞0，
∴2a-b＜0，
∵
∴b+2a=0，
x=-1时，y=a-b+c＜0．
∴
∴3b-2c＞0，
∵抛物线与y轴的正半轴相交，
∴c＞0，
∴3b+2c＞0，
∴P=3b-2c，
Q=b-2a-3b-2c=-2a-2b-2c，
∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-... “抛一枚均匀硬币，落地后正面朝上”这一事件是（ ）
A. 必然事件 B. 随机事件 C. 确定事件 D. 不可能事件
B
【解析】根据随机事件的定义，随机事件就是可能发生，也可能不发生的事件，即可判断：
抛1枚均匀硬币，落地后可能正面朝上，也可能反面朝上，故抛1枚均匀硬币，落地后正面朝上是随机事件.
故选B. 某一型号飞机着陆后滑行的距离y(单位：m)与滑行时间x(单位：s)之间的函数关系式是y＝60x－1.5x2，该型号飞机着陆后需滑行________m才能停下来．
600
【解析】试题分析：∵y=60x﹣1.5x2=﹣1.5（x﹣20）2+600，
∴x=20时，y取得最大值，此时y=600 如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.
（1）操作发现
如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：
①线段DE与AC的位置关系是_________；
②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是____________.
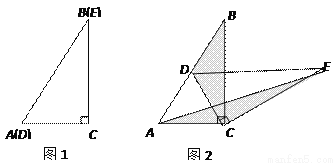
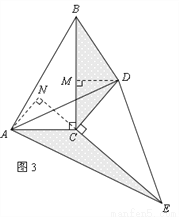
（2）猜想论证
当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想.
（3）拓展探究
已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE//AB交BC于点E（如图4）.若在射线BA上存在点F，使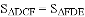
，请直接写出相应的BF的长.
（1）①DE∥AC；②S1＝S2；（2）证明见解析；（3）BF的长为或.
【解析】试题分析：（1）①根据旋转的性质可得AC=CD，然后求出△ACD是等边三角形，根据等边三角形的性质可得∠ACD=60°，然后根据内错角相等，两直线平行解答；
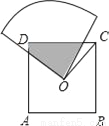
②根据等边三角形的性质可得AC=AD，再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=AB，然后求出AC=BD，再根据等边三角形的性质求... 如图，O是边长为a的正方形ABCD的中心，将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处，并将纸板的圆心绕O旋转，则正方形ABCD被纸板覆盖部分的面积为（ ）
A. 
a2 B. 
a2 C. 
a2 D. 
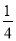a
B
【解析】【解析】
扇形的半径交AD于E，交CD于F，连结OD，如图．
∵四边形ABCD为正方形，∴OD=OC，∠COD=90°，∠ODA=∠OCD=45°．
∵∠EOF=90°，即∠EOD+∠DOF=90°，∠DOF+∠COF=90°，∴∠EOD=∠FOC．
在△ODE和△OCF中，∵∠ODE=∠OCF，OD=OC，∠EOD=∠COF，∴△ODE≌△OCF，∴S△OD... 一个图形无论经过平移变换，还是经过旋转变换，下列说法正确的是（ ）
①对应线段平行
②对应线段相等
③图形的形状和大小都没有发生变化
④对应角相等．
A. ①②③ B. ②③④ C. ①②④ D. ①③④
B
【解析】【解析】
①平移后对应线段平行，旋转对应线段不一定平行，故本小题错误；
②无论平移还是旋转，对应线段相等，故本小题正确；
③无论平移还是旋转，图形的形状和大小都没有发生变化，故本小题正确；
④无论平移还是旋转，对应角相等，故本小题正确．
综上所述，说法正确的是②③④．
故选B． 如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）
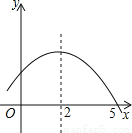
A. -1＜x＜5 B. x＞5 C. x＜-1且x＞5 D. x＜-1或x＞5
D
【解析】由图可知，抛物线的对称轴为直线x=2，与x轴的一个交点坐标为（5，0），
∴函数图象与x轴的另一交点坐标为（-1，0），
∴ax2+bx+c＜0的解集是x＜-1或x＞5．
故选C. 等腰三角形的周长为24cm，腰长为xcm，则x的取值范围是( )
A. x＜6 B. 6＜x＜12 C. 0＜x＜12 D. x＞12
B
【解析】等腰三角形的周长为24cm，腰长为xcm，则底边长为24-2x，
根据三边关系，x+x＞24-2x，解得，x＞6；
x-x＜24-2x，解得，x＜12，
所x的取值范围是6＜x＜12．
故选：C．