题目内容
1.计算:(1)(2x+3y)2-(4x-9y)(4x+9y)+(2x-3y)2;
(2)(3x-2y)2-(4y-3x)(3x+4y);
(3)(x+2y-1)(x-2y+1)-(x-2y-1)2.
分析 (1)先利用完全平方公式计算(2x+3y)2,(2x-3y)2,利用平方差公式计算(4x-9y)(4x+9y),再去括号、合并同类项即可;
(2)先利用完全平方公式计算(3x-2y)2,利用平方差公式计算(4y-3x)(3x+4y),再去括号、合并同类项即可;
(3)先利用平方差公式计算(x+2y-1)(x-2y+1),利用完全平方公式计算(x-2y-1)2,再去括号、合并同类项即可.
解答 解:(1)(2x+3y)2-(4x-9y)(4x+9y)+(2x-3y)2
=(4x2+12xy+9y2)-(16x2-81y2)+(4x2-12xy+9y2)
=4x2+12xy+9y2-16x2+81y2+4x2-12xy+9y2
=-8x2+18y2;
(2)(3x-2y)2-(4y-3x)(3x+4y);
=9x2-12xy+4y2-16y2+9x2
=188x2-12xy-12y2;
(3)(x+2y-1)(x-2y+1)-(x-2y-1)2
=x2-(2y-1)2-[x2-2x(2y+1)+(2y-1)2]
=x2-4y2+4y-1-[x2-4xy-2x+4y2-4y+1]
=x2-4y2+4y-1-x2+4xy+2x-4y2+4y-1
=-8y2+8y+4xy+2x-2.
点评 本题主要考查完全平方公式和平方差公式,熟记公式结构是解题的关键.完全平方公式:(a±b)2=a2±2ab+b2;平方差公式:(a+b)(a-b)=a2-b2.

练习册系列答案
相关题目
12.近似数2.60所表示的精确值x的取值范围( )
| A. | 2.600<x≤2.605 | B. | 2.595<x≤2.605 | C. | 2.595≤x<2.605 | D. | 2.50≤x<2.70 |
6.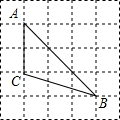 如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
 如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).(结果保留根号)
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).(结果保留根号)