题目内容
 已知:如图∠BAC的角平分线与BC的垂直平分线交与点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.
已知:如图∠BAC的角平分线与BC的垂直平分线交与点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:
分析:连接BD、CD,根据垂直平分线性质可得BD=CD,可证RT△BDE≌RT△CDF,可得BE=CF.
解答:解:连接BD、CD,根据垂直平分线性质可得BD=CD,

∵D为∠BAC上面的点,DE⊥AB,DF⊥AC
∴DE=DF,
在RT△BDE和RT△CDF中,
,
∴RT△BDE≌RT△CDF(HL),
∴BE=CF.

∵D为∠BAC上面的点,DE⊥AB,DF⊥AC
∴DE=DF,
在RT△BDE和RT△CDF中,
|
∴RT△BDE≌RT△CDF(HL),
∴BE=CF.
点评:本题考查了直角三角形全等的判定,考查了垂直平分线的性质,考查了角平分线的性质,本题中求证RT△BDE≌RT△CDF是解题的关键.

练习册系列答案
相关题目
 如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
如图,AD=BC,AC=BD,则下列结论中,不正确的是( )| A、OA=OB |
| B、∠AOB=∠C+∠D |
| C、CO=DO |
| D、∠C=∠D |
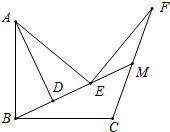 如图,AB=BC,∠ABC=90°,∠ABE=∠AEB,AD⊥BE,AE=EF,∠AEF=90°,CF交BE延长线于点M,探究FM与CM的数量关系.
如图,AB=BC,∠ABC=90°,∠ABE=∠AEB,AD⊥BE,AE=EF,∠AEF=90°,CF交BE延长线于点M,探究FM与CM的数量关系. 已知:DA⊥AB,CA⊥AE,AB=AE,AC=AD,求证:DE=BC.
已知:DA⊥AB,CA⊥AE,AB=AE,AC=AD,求证:DE=BC. 如图,点C、E、B、F在同一直线上,AC∥DF,∠A=∠D,CE=BF.求证:AB=DE.
如图,点C、E、B、F在同一直线上,AC∥DF,∠A=∠D,CE=BF.求证:AB=DE. 如图,已知E是等腰梯形ABCD的腰BC的中点,AE把梯形分成四边形AECD和△AEB,且四边形AECD的周长比△AEB周长要多4cm,若AB=12cm,CD=2cm,求梯形的腰AD长.
如图,已知E是等腰梯形ABCD的腰BC的中点,AE把梯形分成四边形AECD和△AEB,且四边形AECD的周长比△AEB周长要多4cm,若AB=12cm,CD=2cm,求梯形的腰AD长.