题目内容
反比例函数y=
的图象经过A(m-1,m+1)、B(2m-1,
)两点,直线AO交双曲线于另一点C.D为x轴上一动点,过A点作直线AE⊥CD于E,交y轴于F点,连接FD.在D点运动过程中,试判断以线段AF,CD,DF的长为边的三角形的形状,并说明理由.
| k |
| x |
| m |
| 2 |
考点:反比例函数综合题
专题:
分析:首先利用待定系数法求得A、B的坐标,点D的坐标是(m,0),求得直线AE的解析式,即可求得F的坐标,然后表示出AF2、CD2、DF2的长,利用勾股定理的逆定理判断.
解答:解:根据题意得:(m-1)(m+1)=(2m-1)•
=k,
解得:m=2,k=3,
则A的坐标是(1,3),B的坐标是(3,1).
设D的坐标是(m,0),
则CD2=(m+1)2+32=m2+2m+10,
设直线CD的解析式是:y=kx+b,
根据题意得:
,
解得:k=
,
∵AE⊥CD,
∴设直线AE的解析式是:y=-
x+c,
把(1,3)代入解析式,得:c=
,
则直线AE的解析式是:y=-
+
,
令x=0,解得y=
,即F的坐标是(0,
).
则AF2=1+(
-3)2=
-2m-10,
DF2=m2+(
)2=m2+
.
又∵CD2=m2+2m+10,
∴CD2+AF2=DF2.
∴以线段AF,CD,DF的长为边的三角形是以DF为斜边的直角三角形.
| m |
| 2 |
解得:m=2,k=3,
则A的坐标是(1,3),B的坐标是(3,1).
设D的坐标是(m,0),
则CD2=(m+1)2+32=m2+2m+10,
设直线CD的解析式是:y=kx+b,
根据题意得:
|
解得:k=
| 3 |
| m+1 |
∵AE⊥CD,
∴设直线AE的解析式是:y=-
| m+1 |
| 3 |
把(1,3)代入解析式,得:c=
| m+10 |
| 3 |
则直线AE的解析式是:y=-
| m+1 |
| 3 |
| m+10 |
| 3 |
令x=0,解得y=
| m+10 |
| 3 |
| m+10 |
| 3 |
则AF2=1+(
| m+10 |
| 3 |
| m2+20m+100 |
| 9 |
DF2=m2+(
| m+10 |
| 3 |
| m2+20m+100 |
| 9 |
又∵CD2=m2+2m+10,
∴CD2+AF2=DF2.
∴以线段AF,CD,DF的长为边的三角形是以DF为斜边的直角三角形.
点评:本题考查了待定系数法求反比例函数的解析式,以及两点之间距离公式的求法,以及两直线垂直的条件,利用m表示出F的坐标是关键.

练习册系列答案
相关题目
下列说法错误的是( )
A、
| ||||
B、当x<2时,
| ||||
C、当x<0时,
| ||||
D、
|
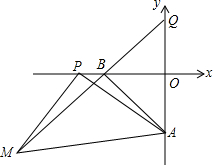 在平面直角坐标系中,A(0,-5),B(-5,0),P为x轴上B点左侧的一个动点,以AP为边作等腰直角三角形APM,其中PA=PM,∠APM=90°,MB交y轴于Q,当P在x轴上运动时,线段OQ的长度是否变化?若不变,求其值;若变化,求其变化范围.
在平面直角坐标系中,A(0,-5),B(-5,0),P为x轴上B点左侧的一个动点,以AP为边作等腰直角三角形APM,其中PA=PM,∠APM=90°,MB交y轴于Q,当P在x轴上运动时,线段OQ的长度是否变化?若不变,求其值;若变化,求其变化范围.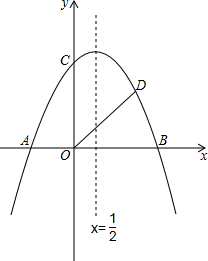 如图,抛物线y=-
如图,抛物线y=- 已知:如图,AB=AD,CB=CD,E是AC上一点,求证:EB=ED.
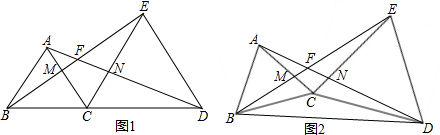
已知:如图,AB=AD,CB=CD,E是AC上一点,求证:EB=ED. 已知:如图∠BAC的角平分线与BC的垂直平分线交与点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.
已知:如图∠BAC的角平分线与BC的垂直平分线交与点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.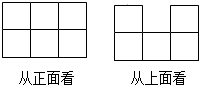 用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.
用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.