Question

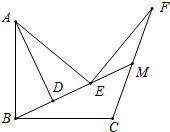如图，AB=BC，∠ABC=90°，∠ABE=∠AEB，AD⊥BE，AE=EF，∠AEF=90°，CF交BE延长线于点M，探究FM与CM的数量关系．

Answer 1

考点：全等三角形的判定与性质

专题：常规题型

分析：过C作CP⊥BM，过F作BM垂线交BM延长线于G点，根据题干中给出的条件可以证明△AED≌△EFG可得FG=DE，可证△ABD≌△BCP，可得CP=BD，进而可以证明△PCM≌△GFM，得FM=CM．

解答：解：过C作CP⊥BM，过F作BM垂线交BM延长线于G点，

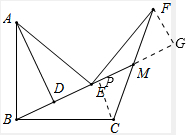
∵∠FEG+∠AED=90°，∠AED+∠EAD=90°，
∴∠EAD=∠FEG，
在△AED和△EFG中，

∠EAD=∠FEG ∠ADE=∠EGF AE=EF

∴△AED≌△EFG（AAS），∴FG=DE，
∵∠ABE+∠CBE=90°，∠PCB+∠CBE=90°，
∴∠PCB=∠ABE，
在△ABD和△BCP中，

∠BPC=∠ADB ∠PCD=∠ABE AB=BC

，
∴△ABD≌△BCP（AAS），∴CP=BD，
∵BD=DE，∴CP=FG，
在△PCM和△GFM中，

∠CMP=∠FMG ∠CPM=∠FGM CP=FG

，
∴△PCM≌△GFM（AAS），
∴FM=CM．

点评：此题考查了全等三角形的判定与性质，考查了全等三角形对应边相等的性质，本题中求证△PCM≌△GFM是解题的关键．