题目内容
8. 如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动时,点B的坐标满足的函数解析式为( )
如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动时,点B的坐标满足的函数解析式为( )| A. | y=-$\frac{1}{x}$(x<0) | B. | y=-$\frac{1}{2x}$(x<0) | C. | y=-$\frac{1}{4x}$(x<0) | D. | y=-$\frac{1}{8x}$(x<0) |
分析 过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,设B点坐标满足的函数解析式是y=$\frac{k}{x}$,易得△AOC∽△OBD,然后由相似三角形面积比等于相似比的平方,求得S△AOC:S△BOD=4,继而求得答案.
解答  解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
设B点坐标满足的函数解析式是y=$\frac{k}{x}$,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∴△AOC∽△OBD,
∴S△AOC:S△BOD=($\frac{AO}{BO}$)2,
∵AO=2BO,
∴S△AOC:S△BOD=4,
∵当A点在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动,
∴S△AOC=$\frac{1}{2}$OC•AC=$\frac{1}{2}$•x•$\frac{2}{x}$=1,
∴S△BOD=$\frac{1}{2}$DO•BD=$\frac{1}{2}$(-x•$\frac{k}{x}$)=-$\frac{1}{2}$k,
∴1=4×(-$\frac{1}{2}$k),解得k=-$\frac{1}{2}$
∴B点坐标满足的函数解析式y=-$\frac{1}{2x}$(x<0).
故选:B.
点评 此题考查了相似三角形的判定与性质以及反比例函数的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
5. 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
16.某工程队计划在10天内修路8km,前两天一共修完了2km,由于计划发生变化,准备提前两天完成修路任务,以后几天内平均每天至少要修路( )
| A. | 1km | B. | 0.9km | C. | 0.8km | D. | 0.6km |
20.桌面上有甲、乙、丙三个杯子,三杯内原本均装有一些水.先将甲杯的水全部倒入丙杯,此时丙杯的水量为原本甲杯内水量的2倍多40毫升;再将乙杯的水全部倒入丙杯,此时丙杯的水量为原本乙杯内水量的3倍少180毫升.若过程中水没有溢出,则原本甲、乙两杯内的水量相差多少毫升?( )
| A. | 80 | B. | 110 | C. | 140 | D. | 220 |
18.下列能用平方差公式计算得是( )
| A. | (-x+y)(x-y) | B. | (y-1)(-1-y) | C. | (x-2)(y+2) | D. | (2x+y)(2y-x) |
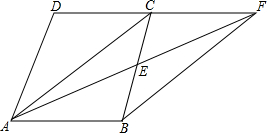 已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.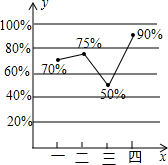 某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题: