题目内容
3.已知A(-1,1),B(-$\frac{1}{2}$,-2),C(-3,-$\frac{1}{3}$)三个点中的两个点在反比例函数图象上.(1)求出这个反比例函数的解析式,并找出不在图象上的点;
(2)设P1(x1,y1),P2(x2,y2)是这个反比例函数图象上任意不重合的两点,M=$\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$,N=$\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$,试判断M,N的大小,并说明理由.
分析 (1)直接根据反比例函数中k=xy的特点进行解答即可.
(2)根据点P的坐标可求出反比例函数的解析式,从而得到y1与x1、y2与x2的关系,然后只需运用作差法就可解决问题.
解答 解:(1)∵A(-1,1),B(-$\frac{1}{2}$,-2),C(-3,-$\frac{1}{3}$),
∴-1×1=-1,(-$\frac{1}{2}$)×(-2)=1,(-3)×(-$\frac{1}{3}$)=1,
∴点A不在这个反比例函数图象上.
(2)M>N.
理由如下∵P1(x1,y1),P2(x2,y2)是函数y=$\frac{1}{x}$图象上的任意不重合的两点,
∴y1=$\frac{1}{{x}_{1}}$,y2=$\frac{1}{{x}_{2}}$,y1≠y2.
∵M=$\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$,N=$\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$,
∴M-N=($\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$)-($\frac{{y}_{2}}{{x}_{1}}$+$\frac{{y}_{1}}{{x}_{2}}$)
=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}}$+$\frac{{y}_{2}-{y}_{1}}{{x}_{2}}$=(y1-y2)($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$)
=(y1-y2)2>0,
∴M>N.
点评 本题主要考查了反比例函数图象上点的坐标特征,在解决问题的过程中用到了数形结合和作差法等重要的数学思想方法,应熟练掌握.

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
 如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动时,点B的坐标满足的函数解析式为( )
如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动时,点B的坐标满足的函数解析式为( )| A. | y=-$\frac{1}{x}$(x<0) | B. | y=-$\frac{1}{2x}$(x<0) | C. | y=-$\frac{1}{4x}$(x<0) | D. | y=-$\frac{1}{8x}$(x<0) |

| A. | 45° | B. | 55° | C. | 125° | D. | 135° |
 为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y万个与生产时间x天之间的函数关系如图所示,则每家企业供应的足球数量a等于1万个.
为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y万个与生产时间x天之间的函数关系如图所示,则每家企业供应的足球数量a等于1万个. 已知线段AB,利用无刻度的直尺和圆规,作线段AC,使点B为线段AC的中点,要求:不写作法,保留作图痕迹.
已知线段AB,利用无刻度的直尺和圆规,作线段AC,使点B为线段AC的中点,要求:不写作法,保留作图痕迹.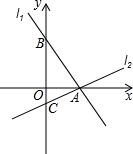 如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.
如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.