题目内容
2.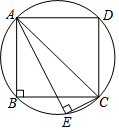 如图,正方形ABCD内接于⊙O,AD=2,弦AE平分BC交BC于P,连接CE,则CE的长为$\frac{2\sqrt{5}}{5}$.
如图,正方形ABCD内接于⊙O,AD=2,弦AE平分BC交BC于P,连接CE,则CE的长为$\frac{2\sqrt{5}}{5}$.
分析 根据圆周角定理求得∠AEC=90°,由勾股定理求出AM的长,再证明△AMB∽△CME,根据相似三角形对应边比例即可求出CE的长.
解答 解:连接AC,BE,如图所示:
∵四边形ABCD是正方形,
∴BC=AB=2,
∵AE平分BC,
∴BM=CM=1, ∵四边形ABCD为圆内正方形,
∵四边形ABCD为圆内正方形,
∴AC必过圆心O,且∠AEC=∠ABC=90°,
∵∠CME=∠AMB,
∴△AMB∽△CME,
∴$\frac{AB}{CE}=\frac{AM}{MC}$.
∵AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴$\frac{2}{CE}=\frac{\sqrt{5}}{1}$,
∴CE=$\frac{2\sqrt{5}}{5}$.
故答案为$\frac{2\sqrt{5}}{5}$.
点评 本题考查了正方形的性质、圆周角定理、相似三角形的判定与性质、勾股定理等知识;证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
12.p+q=0,抛物线y=x2+px+q必经过( )
| A. | (-1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (1,1) |
12.在学习三角形时,李峰同学发现可以折叠出三角形的高,他在折叠其中一个三角形纸片时,只能折叠出一条高,这个纸片的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形或钝角三角形 |
 如图,下列四组条件中:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③AB=DE,AC=DF,∠B=∠E;④∠B=∠E,BC=EF,∠C=∠F.其中不一定能使△ABC≌△DEF的条件是③(只填序号).
如图,下列四组条件中:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③AB=DE,AC=DF,∠B=∠E;④∠B=∠E,BC=EF,∠C=∠F.其中不一定能使△ABC≌△DEF的条件是③(只填序号). (1)圆内接正六边形的边心距为$2\sqrt{3}$,则这个正六边形的面积为24$\sqrt{3}$cm2.
(1)圆内接正六边形的边心距为$2\sqrt{3}$,则这个正六边形的面积为24$\sqrt{3}$cm2. 如图,直线AB、CD相交于点E,DF∥AB,若∠D=70°,则∠CEB的度数为110°.
如图,直线AB、CD相交于点E,DF∥AB,若∠D=70°,则∠CEB的度数为110°.