题目内容
17. (1)圆内接正六边形的边心距为$2\sqrt{3}$,则这个正六边形的面积为24$\sqrt{3}$cm2.
(1)圆内接正六边形的边心距为$2\sqrt{3}$,则这个正六边形的面积为24$\sqrt{3}$cm2.(2)如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了1000米.
分析 (1)根据正六边形的特点,通过中心作边的垂线,连接半径,结合解直角三角形的有关知识解决;
(2)过点B作BC⊥水平面于点C,在Rt△ABC中,根据AB=200米,∠A=30°,求出BC的长度即可.
解答 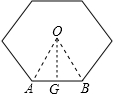 解:(1)如图,连接OA、OB;过点O作OG⊥AB于点G.
解:(1)如图,连接OA、OB;过点O作OG⊥AB于点G.
在Rt△AOG中,OG=2$\sqrt{3}$,∠AOG=30°,
∵OG=OA•cos30°,
∴OA=$\frac{OG}{cos30°}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4,
∴这个正六边形的面积为6×$\frac{1}{2}$×4×2$\sqrt{3}$=24$\sqrt{3}$.
故答案为:24$\sqrt{3}$; (2)过点B作BC⊥水平面于点C,
(2)过点B作BC⊥水平面于点C,
在Rt△ABC中,
∵AB=2000米,∠A=30°,
∴BC=ABsin30°=2000×$\frac{1}{2}$=1000(米).
故答案为1000.
点评 本题考查了解直角三角形的应用-坡度坡角问题,解答本题的关键是根据坡角构造直角三角形,利用三角函数的知识进行求解.也考查了正多边形和圆.

练习册系列答案
相关题目
8. 如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )
如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )
 如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )
如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )| A. | 4$\sqrt{3}$米 | B. | (2$\sqrt{3}$+2)米 | C. | (4$\sqrt{2}$-4)米 | D. | (4$\sqrt{3}$-4)米 |
12.根据图中提供的信息,可知一个杯子的价格是( )


| A. | 50元 | B. | 30元 | C. | 20元 | D. | 8元 |
6.若抛物线的图象经过A(0,3),B(2,0),C(0,-2),D(5,3)中的三个点,则关于该抛物线的叙述正确的是( )
| A. | 不经过点A | B. | 不经过点B | ||
| C. | 开口向下 | D. | 顶点为(2.5,-0.125) |
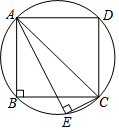 如图,正方形ABCD内接于⊙O,AD=2,弦AE平分BC交BC于P,连接CE,则CE的长为$\frac{2\sqrt{5}}{5}$.
如图,正方形ABCD内接于⊙O,AD=2,弦AE平分BC交BC于P,连接CE,则CE的长为$\frac{2\sqrt{5}}{5}$. 尺规作图.如图,△ABC,点M是AB边的中点,过点M作BC边的平行线.(保留作图痕迹,不写作法).
尺规作图.如图,△ABC,点M是AB边的中点,过点M作BC边的平行线.(保留作图痕迹,不写作法).