题目内容
6. 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | (-1,1) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
分析 根据图形和已知条件可以求得点A的坐标,由等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,进而得到A′的坐标.
解答 解:∵三角形AOB是等腰直角三角形,点B的横坐标为2,
∴OA=AB,∠OAB=90°,OB=2,
∴OA=AB=$\sqrt{2}$,
∴点A的坐标为(1,1),
∵等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,
∴点A′的坐标为(-1,1),
故选C.
点评 本题考查直角三角形的性质、坐标与图形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
19.下列运算正确的是( )
| A. | 6a-5a=1 | B. | a2•a3=a5 | C. | (a2)3=a5 | D. | a6÷a3=a2 |
20.计算(x+1)(x2+1)(x4+1)(x8+1)(x-1)=xn-1,则n等于( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
18. 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,
l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则$\frac{DE}{EF}$的值为
( )
 如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,
如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C;直线DF分别交l1,l2,l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则$\frac{DE}{EF}$的值为
( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
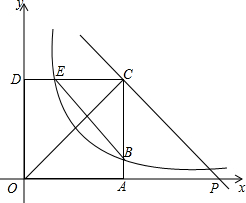 如图所示,点A坐标为(4,0),矩形OACD的两边AC与CD分别交双曲线y=$\frac{4}{x}$(x>0)于B,E两点,记$\frac{BC}{AB}$=k,过点C作CP∥BE交x轴于点P.
如图所示,点A坐标为(4,0),矩形OACD的两边AC与CD分别交双曲线y=$\frac{4}{x}$(x>0)于B,E两点,记$\frac{BC}{AB}$=k,过点C作CP∥BE交x轴于点P.