题目内容
7．已知不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}＞1}\\{x＞m}\end{array}\right.$的解集为x＞2，则（ ）| A． | m＞2 | B． | m＜2 | C． | m=2 | D． | m≤2 |
分析 根据不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}＞1}\\{x＞m}\end{array}\right.$的解集为x＞2，可以求得m的取值范围，从而可以解答本题．
解答 解：由$\left\{\begin{array}{l}{\frac{2x-1}{3}＞1}\\{x＞m}\end{array}\right.$得，$\left\{\begin{array}{l}{x＞2}\\{x＞m}\end{array}\right.$，
∵不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}＞1}\\{x＞m}\end{array}\right.$的解集为x＞2，
∴m≤2，
故选D．
点评 本题考查解一元一次不等式组，解答本题的关键是明确一元一次不等式组的解答方法．
练习册系列答案
春雨教育同步作文系列答案
相关题目
17．如果一个角的补角等于它余角的4倍，那么这个角的度数是（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
18．“南海”在过去的2016年中出镜率非常高，为了让学生了解南海，关注南海．某校举办了南海有关知识比赛，唐老师对名列前20名的选手的得分x进行分组统计，结果如表所示：
（1）求b的值
（2）若用扇形图来描述，求分值在8≤m＜9范围内所对应的扇形图的圆心角大小；
（3）若唐老师从第一粗和第三组这4名同学中随机选取2名同学进行座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）
| 组号 | 分值 | 频数 |
| 一 | 6≤m＜7 | 2 |
| 二 | 7≤m＜8 | 8 |
| 三 | 8≤m＜9 | a |
| 四 | 9≤m≤10 | b |
（2）若用扇形图来描述，求分值在8≤m＜9范围内所对应的扇形图的圆心角大小；
（3）若唐老师从第一粗和第三组这4名同学中随机选取2名同学进行座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）
12．
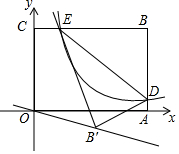如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数y=$\frac{6}{x}$的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（ ）
如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数y=$\frac{6}{x}$的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（ ）| A． | $-\frac{2}{5}$ | B． | $-\frac{1}{21}$ | C． | $-\frac{1}{5}$ | D． | $-\frac{1}{24}$ |
