题目内容
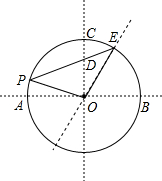 如图,AB是⊙O的直径,OC是垂直于AB的半径,过弧AC上一点P作弦PE,分别交OC和
如图,AB是⊙O的直径,OC是垂直于AB的半径,过弧AC上一点P作弦PE,分别交OC和 |
| BC |
 |
| AP |
 |
| BE |
考点:圆周角定理
专题:
分析:设∠AOP=x°,求出∠POC=(90-x)°,根据等腰三角形性质和三角形内角和定理求出∠PDO=∠POC=(90-x)°,求出∠P=2x°∠P=∠OEP=2x°,∠POE=(180-4x)°,求出∠BOE=3x°=3∠AOP,即可求出答案.
解答:解:设∠AOP=x°,
∵CO⊥AB,
∴∠AOC=90°,
∴∠POC=(90-x)°,
∵PO=PD,
∴∠PDO=∠POC=(90-x)°,
∴∠P=180°-∠POD-∠PDO=2x°,
∵PO=OE,
∴∠P=∠OEP=2x°,
∴∠POE=180°-∠P-∠OEP=(180-4x)°,
∴∠BOE=180°-∠AOP-∠POE=3x°=3∠AOP,
∴3
=
.

∵CO⊥AB,
∴∠AOC=90°,
∴∠POC=(90-x)°,
∵PO=PD,
∴∠PDO=∠POC=(90-x)°,
∴∠P=180°-∠POD-∠PDO=2x°,
∵PO=OE,
∴∠P=∠OEP=2x°,
∴∠POE=180°-∠P-∠OEP=(180-4x)°,
∴∠BOE=180°-∠AOP-∠POE=3x°=3∠AOP,
∴3
 |
| AP |
 |
| BE |
点评:本题考查了圆心角、弧、弦之间的关系,等腰三角形的性质,三角形内角和定理的应用,解此题的关键是求出∠BOE=3∠AOP.

练习册系列答案
相关题目
 如图,在△ABC中,点D、E分别在BC、AC上,BE平分∠ABC,DE∥BA,如果CE=10,AE=6,△CDE的周长为34,求DE的长.
如图,在△ABC中,点D、E分别在BC、AC上,BE平分∠ABC,DE∥BA,如果CE=10,AE=6,△CDE的周长为34,求DE的长.