题目内容
如图，在△ABC中，点D、E分别在BC、AC上，BE平分∠ABC，DE∥BA，如果CE=10，AE=6，△CDE的周长为34，求DE的长．考点：等腰三角形的判定与性质,平行线的性质
专题：
分析：根据角平分线定义以及平行线的性质，可得△BDE为等腰三角形，即BD=DE，又因为DE∥BA，得
=
，计算BD的长即可．
| BD |
| BC |
| AE |
| AC |
解答：解：∵DE∥BA
∴∠ABE=∠DEB
∵BE平分∠ABC
∴∠ABE=∠DBE
∴∠DBE=∠DEB
∴BD=DE
∴DE+DC=BD+DC=BC，
∵△CDE的周长=DE+DC+EC=BC+CE=34，CE=10，AE=6，
∴BC=34-10=24，AC=AE+CE=16，
∵DE∥BA
∴
=
，
即
=
，
∴BD=9，
∴DE=9．
∴∠ABE=∠DEB
∵BE平分∠ABC
∴∠ABE=∠DBE
∴∠DBE=∠DEB
∴BD=DE
∴DE+DC=BD+DC=BC，
∵△CDE的周长=DE+DC+EC=BC+CE=34，CE=10，AE=6，
∴BC=34-10=24，AC=AE+CE=16，
∵DE∥BA
∴
| BD |
| BC |
| AE |
| AC |
即
| BD |
| 24 |
| 6 |
| 16 |
∴BD=9，
∴DE=9．
点评：此题综合运用了平行线的性质、等腰三角形的判定、平行线分线段成比例定理．
练习册系列答案
阅读快车系列答案
相关题目
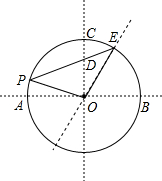如图，AB是⊙O的直径，OC是垂直于AB的半径，过弧AC上一点P作弦PE，分别交OC和
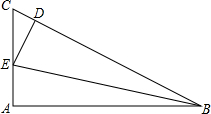在直角△ABC中，∠A=90°，∠ABC的平分线BE交AC于E点，过E点作ED⊥BC于D点，已知AC=10cm，△CDE的周长为16cm，求：CD的长．