题目内容
已知a=
(
+1),求
.
| 1 |
| 2 |
| 5 |
| a3+a+a |
| a5 |
考点:二次根式的化简求值
专题:计算题
分析:先由a=
(
+1)变形得到2a-1=
,两边平分整理得a2=a+1,再利用降次的方法计算表示出a3=2a+1,a5=5a+3,则原式=
,再把a的值代入后分母有理化即可.
| 1 |
| 2 |
| 5 |
| 5 |
| 4a+1 |
| 5a+1 |
解答:解:∵a=
(
+1),
∴2a-1=
,
∴(2a-1)2=5,即a2-a-1=0,
∴a2=a+1,
∴a3=a(a+1)=a2+a=a+1+a=2a+1,
a5=a2•a3=(a+1)(2a+1)=5a+3,
∴原式=
=
=
=
=
.
| 1 |
| 2 |
| 5 |
∴2a-1=
| 5 |
∴(2a-1)2=5,即a2-a-1=0,
∴a2=a+1,
∴a3=a(a+1)=a2+a=a+1+a=2a+1,
a5=a2•a3=(a+1)(2a+1)=5a+3,
∴原式=
| 2a+1+a+a |
| 5a+1 |
=
| 4a+1 |
| 5a+1 |
=
4×
| ||||
5×
|
=
4
| ||
5
|
=
29+
| ||
| 38 |
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
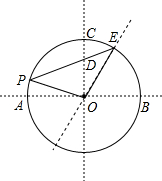 如图,AB是⊙O的直径,OC是垂直于AB的半径,过弧AC上一点P作弦PE,分别交OC和
如图,AB是⊙O的直径,OC是垂直于AB的半径,过弧AC上一点P作弦PE,分别交OC和
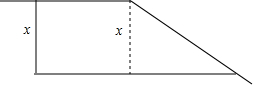 如图,要建立一个形状是直角梯形的存料场,其中两边是夹角为150°的两面墙,另外两边是总长为30m的篱笆,问篱笆两边各是多少米时,存料场的面积最大?最大面积是多少?
如图,要建立一个形状是直角梯形的存料场,其中两边是夹角为150°的两面墙,另外两边是总长为30m的篱笆,问篱笆两边各是多少米时,存料场的面积最大?最大面积是多少? 如图,在四边形ABCD中,AB=CD,AD=BC,延长DA到M,延长BC至N,使AM=CN,求证:AN=CM.
如图,在四边形ABCD中,AB=CD,AD=BC,延长DA到M,延长BC至N,使AM=CN,求证:AN=CM.