题目内容
三个相同的骰子,6个面,每个面上分别标有1、2、3、4、5、6,随机抛下
(1)只出现一个1的概率是多少?
(2)出现两个1的概率是多少?
(3)出现三个1的概率是多少?
(4)不出现1的概率是多少?
(1)只出现一个1的概率是多少?
(2)出现两个1的概率是多少?
(3)出现三个1的概率是多少?
(4)不出现1的概率是多少?
考点:列表法与树状图法
专题:
分析:(1)三个骰子同时抛出,一共有6×6×6=216种情况,由此可求出只出现一个1的概率;
(2)三个骰子同时抛出,一共有6×6×6=216种情况,由此可求出出现两个1的概率的概率;
(3)三个骰子同时抛出,一共有6×6×6=216种情况,由此可求出出现三个1的概率的概率;
(4)由(1),(2),(3)中的概率即可求出不出现1的概率.
(2)三个骰子同时抛出,一共有6×6×6=216种情况,由此可求出出现两个1的概率的概率;
(3)三个骰子同时抛出,一共有6×6×6=216种情况,由此可求出出现三个1的概率的概率;
(4)由(1),(2),(3)中的概率即可求出不出现1的概率.
解答:解(1)只出现一个1的概率是:
×(1-
)×(1-
)×3=
;.
(2)出现两个1的概率是:
×
×(1-
)×3=
;
(3)出现三个1的概率是:
;
(4)∵P(三个色子一起摇一次出现1的概率)=
+
+
=
,
∴出现1的概率是1-
=
.
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 75 |
| 216 |
(2)出现两个1的概率是:
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 15 |
| 216 |
(3)出现三个1的概率是:
| 1 |
| 216 |
(4)∵P(三个色子一起摇一次出现1的概率)=
| 1 |
| 216 |
| 15 |
| 216 |
| 75 |
| 216 |
| 91 |
| 216 |
∴出现1的概率是1-
| 91 |
| 216 |
| 125 |
| 216 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
 如图,在△ABC中,BC=2,BC∥x轴,点B的坐标是(-3,1),点A的坐标是(-4,3).
如图,在△ABC中,BC=2,BC∥x轴,点B的坐标是(-3,1),点A的坐标是(-4,3).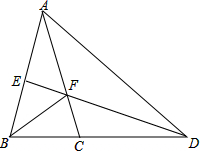 △ABC是黄金三角形,BF平分∠ABC交AC于F,取AB中点E,连接EF交BC延长线于M,连接AM,说明△MAB是黄金三角形.
△ABC是黄金三角形,BF平分∠ABC交AC于F,取AB中点E,连接EF交BC延长线于M,连接AM,说明△MAB是黄金三角形.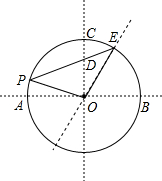 如图,AB是⊙O的直径,OC是垂直于AB的半径,过弧AC上一点P作弦PE,分别交OC和
如图,AB是⊙O的直径,OC是垂直于AB的半径,过弧AC上一点P作弦PE,分别交OC和