Question

6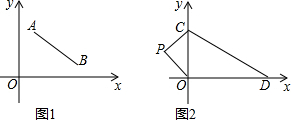．已知，在平面直角坐标系中，A（1，a），B（b，1），其中a，b满足$\sqrt{2a-b-2}$+（a+b-7）²=0．
（1）求a，b的值；
（2）平移线段AB至CD，其中A，B的对应点分别为C，D．
①若CD所在的直线过O点，求将AB向下平移了多少个单位长度？
②如图2，若C，D两点的坐标分别为C（0，c），D（d，0），点P（m，1）是第二象限内一点，且m为整数，动点Q在线段DO上以1个单位/秒的速度从D出发向O运动，运到O点停止，若S_△POQ=S_△COP，且S_{四边形CDOP}≥2S_△COP，请求出点Q的运动时间．

Answer 1

分析 （1）根据算术平方根和平方的非负性建立方程组求解即可；
（2）①利用待定系数法求出直线AB的解析式即可得出结论；
②根据平移的性质得出点C，D坐标，再再利用三角形面积公式即可得出结论．

解答 解：（1）∵a，b满足$\sqrt{2a-b-2}$+（a+b-7）²=0．∴2a-b-2=0，a+b-7=0，
∴a=3，b=4；
（2）①如图1，∵a=3，b=4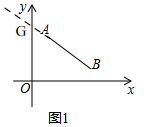，∴A（1，3），B（4，1），
设直线AB的解析式为y=kx+b，∴$\left\{\begin{array}{l}{k+b=3}\\{4k+b=1}\end{array}\right.$，∴$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=\frac{11}{3}}\end{array}\right.$，
延长BA与y轴交于G点，∴G（0，$\frac{11}{3}$），故可知AB向下平移了$\frac{11}{3}$个单位．
②∵平移线段AB至CD，其中A（1，3），B（4，1）的对应点分别为C，D，
∴直线AB向下平移1个单位向左平移一个单位到底如图位置，
则C（0，2），D（3，0），
设Q的运动时间为t秒，则DQ=t，OQ=3-t，
∵S_△POQ=S_△COP
∴3-t=2×（-m），即t=3+2m
又∵S_{四边形CDOP}≥2S_△COP
∴2×3+2×（-m）≥2×2×（-m）
∴m≥-3
又∵点P（m，1）是第二象限内一点，且m为整数
∴m=-3，-2或-1
而t=3+2m＞0，故m=-1，t=1
故Q的运动时间为1秒．

点评 此题是四边形综合题，主要考查了非负性，方程组的解法，待定系数法，平移的性质，几何图形的面积的计算方法，解本题的关键是利用待定系数法求出直线AB的解析式．