题目内容
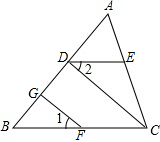 如图,在△ABC中,CD⊥AB于点D,FG⊥AB于点G,∠1=∠2,问DE与BC的关系如何,为什么?
如图,在△ABC中,CD⊥AB于点D,FG⊥AB于点G,∠1=∠2,问DE与BC的关系如何,为什么?答:DE与BC
理由如下:∵CD⊥AB,FG⊥AB( )
∴∠BGF=
∴GF∥DC( )
又∠BDC+∠DCB+∠B=180°( )
∠BGF+∠1+∠B=180°( )
∴∠1=
又∠1=∠2( )
∴∠2=
∴
考点:平行线的判定与性质
专题:推理填空题
分析:根据垂直定义得出∠BGF=∠BDC=90°,根据平行线的判定得出GF∥DC,根据平行线的性质得出∠1=∠BCD,求出∠2=∠BCD即可.
解答:
解:DE∥BC,
理由是:CD⊥AB,FG⊥AB(已知),
∴∠BGF=∠BDC=90°(垂直的定义),
∴GF∥DC(同位角相等,两直线平行),
∴∠1=∠BCD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠2=∠BCD(等量代换),
∴DE∥BC(内错角相等,两直线平行),
故答案为:平行,∠BDC,∠BCD,∠BCD,DE,BC.
理由是:CD⊥AB,FG⊥AB(已知),
∴∠BGF=∠BDC=90°(垂直的定义),
∴GF∥DC(同位角相等,两直线平行),
∴∠1=∠BCD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠2=∠BCD(等量代换),
∴DE∥BC(内错角相等,两直线平行),
故答案为:平行,∠BDC,∠BCD,∠BCD,DE,BC.
点评:本题考查了平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则与点C所表示的数最接近的整数是( )

| A、2 | B、1 | C、0 | D、-1 |
抛物线y=-2x2+3x+2与y轴的交点坐标为( )
| A、(2,2) |
| B、(-2,2) |
| C、(0,2) |
| D、(2,0) |
 如图,AB是⊙O的直径,CD是弦,且AB⊥CD,若∠BOC=50°,则∠A=
如图,AB是⊙O的直径,CD是弦,且AB⊥CD,若∠BOC=50°,则∠A=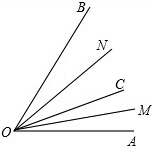 如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线
如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线 小刚在研究矩形性质时,把两张完全相同的矩形纸片叠放在一起(如图中矩形ABCD和矩形BFDE),请你帮他判断重叠部分的四边形BNDM的性状,并给出证明.
小刚在研究矩形性质时,把两张完全相同的矩形纸片叠放在一起(如图中矩形ABCD和矩形BFDE),请你帮他判断重叠部分的四边形BNDM的性状,并给出证明. 如图,直线y=x+4与抛物线y=-x2+10相交于A(2,6),B(-3,1)两点,与y轴相交于点C,过点C作直线l交抛物线于E、F两点,是否存在直线l,使S△EOC:S△FOC=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
如图,直线y=x+4与抛物线y=-x2+10相交于A(2,6),B(-3,1)两点,与y轴相交于点C,过点C作直线l交抛物线于E、F两点,是否存在直线l,使S△EOC:S△FOC=1:3?若存在,求直线l的解析式;若不存在,请说明理由. 如图,已知∠ADE=70°,DF平分∠ADE,∠1=35°,求证:DF∥BE.
如图,已知∠ADE=70°,DF平分∠ADE,∠1=35°,求证:DF∥BE.