题目内容
 如图,直线y=x+4与抛物线y=-x2+10相交于A(2,6),B(-3,1)两点,与y轴相交于点C,过点C作直线l交抛物线于E、F两点,是否存在直线l,使S△EOC:S△FOC=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
如图,直线y=x+4与抛物线y=-x2+10相交于A(2,6),B(-3,1)两点,与y轴相交于点C,过点C作直线l交抛物线于E、F两点,是否存在直线l,使S△EOC:S△FOC=1:3?若存在,求直线l的解析式;若不存在,请说明理由.考点:二次函数的性质,待定系数法求一次函数解析式
专题:
分析:由直线y=x+4与y轴的交点坐标C为(0,4),根据直线l过点C,设直线l的解析式为y=kx+4,根据题意设E(a,-a2+10),F(-3a,-9a2+10),代入直线l的解析式y=kx+4,即可求得k的值,进而求得直线l的解析式.
解答:
解:设E(a,-a2+10),
∵S△EOC:S△FOC=1:3,
∴F(-3a,-9a2+10),
∵直线y=x+4与y轴的交点坐标为(0,4),
∴设直线l的解析式为y=kx+4,
把E、F代入得
,
解得k=±2
,
∴直线l的解析式为y=2
x+4或y=-2
x+4.
∵S△EOC:S△FOC=1:3,
∴F(-3a,-9a2+10),
∵直线y=x+4与y轴的交点坐标为(0,4),
∴设直线l的解析式为y=kx+4,
把E、F代入得
|
解得k=±2
| 2 |
∴直线l的解析式为y=2
| 2 |
| 2 |
点评:本题考查了二次函数的性质,待定系数法求一次函数的解析式,分析出E、F两点的横坐标的特点是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
下列语句中:
①一个锐角与一个钝角互补;
②一个角的补角一定大于这个角;
③如果两个角互余且相等,那么这两个角都等于45°;
④过一点有且只有一条直线与已知直线平行.
其中正确的是( )
①一个锐角与一个钝角互补;
②一个角的补角一定大于这个角;
③如果两个角互余且相等,那么这两个角都等于45°;
④过一点有且只有一条直线与已知直线平行.
其中正确的是( )
| A、①②③④ | B、②③④ |
| C、③④ | D、只有③ |
在下面的分式变形中,不正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
 如图所示,△ABC≌△DEF,DF和AC,FE和CB是对应边.若∠A=100°,∠F=47°,则∠B的度数是( )
如图所示,△ABC≌△DEF,DF和AC,FE和CB是对应边.若∠A=100°,∠F=47°,则∠B的度数是( )| A、33° | B、47° |
| C、53° | D、100° |
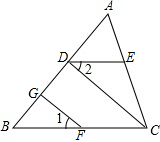 如图,在△ABC中,CD⊥AB于点D,FG⊥AB于点G,∠1=∠2,问DE与BC的关系如何,为什么?
如图,在△ABC中,CD⊥AB于点D,FG⊥AB于点G,∠1=∠2,问DE与BC的关系如何,为什么? (1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平于EF(
(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平于EF(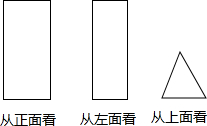 已知如图是三个方向看到的一个几何体的形状.
已知如图是三个方向看到的一个几何体的形状. 如图,已知PE∥AB,PE交BC于E,PF∥CB,PF交BA于F,PH⊥BA,垂足为点H,∠CEP=43°,求∠FPH的度数.
如图,已知PE∥AB,PE交BC于E,PF∥CB,PF交BA于F,PH⊥BA,垂足为点H,∠CEP=43°,求∠FPH的度数.