题目内容

如图，AB是⊙O的直径，CD是弦，且AB⊥CD，若∠BOC=50°，则∠A=
 
°．
考点：圆周角定理,垂径定理
专题：
分析：连接OD，由AB为⊙O的直径，CD为弦，AB⊥CD，根据垂径定理的即可求得
BC
=
BD
，进而可得∠DOB=∠BOC=50°，然后由圆周角定理，即可求得答案．
解答： 解：连接OD，

∵AB为⊙O的直径，CD为弦，AB⊥CD，
∴
BC
=
BD
，
∴∠DOB=∠BOC=50°，
∴∠A=
1
2
∠DOB=25°．
故答案为：25．
点评：此题考查了圆周角定理，在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．同时也考查了垂径定理，垂直于弦的直径平分弦及弦所对的弧．
练习册系列答案
相关题目
如图，在平面直角坐标系中，已知点A（0，4）、B（-4，0），BE⊥AC于E交y轴于点M（0，a），且∠BMA=105°．下列四个结论：①AE=
1
2
AB；②点C的坐标为（2a，0）；③AB=CM+BM；④CE+CM=AE．其中结论正确的序号是（　　）
A、只有①④B、只有①③④
C、只有②③D、①②③④
如图，在Rt△ABC中，BC=（2+
3
）cm，∠B=15°，求AC的长．
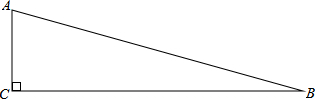
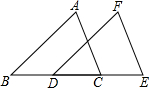如图，△ABC沿直线l向右移了3厘米，得△FDE，且BC=6厘米，∠B=40°．
（1）求BE；
（2）求∠FDB的度数；
（3）找出图中相等的线段（不另添加线段）；
（4）找出图中互相平行的线段（不另添加线段）
如图，点A，B，C在⊙O上，连接AB，AC，若∠BOC=100°，则∠B+∠C的度数为（　　）
A、25°B、50°
C、100°D、无法计算
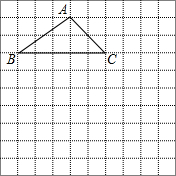如图所示，在10×10正方形网格中，△ABC的三个顶点都在格点上，请按下列要求画图并回答问题：
（1）画出将△ABC先向右平移3格，再向下平移5格后得到的△A1B1C1；
（2）作△ABC的中线AD，△ACD的中线DE；
（3）若△CDE的面积等于2，那么△A1B1C1的面积=
 
．
下列语句中：
①一个锐角与一个钝角互补；    
②一个角的补角一定大于这个角；
③如果两个角互余且相等，那么这两个角都等于45°；
④过一点有且只有一条直线与已知直线平行．
其中正确的是（　　）
A、①②③④B、②③④
C、③④D、只有③
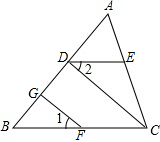如图，在△ABC中，CD⊥AB于点D，FG⊥AB于点G，∠1=∠2，问DE与BC的关系如何，为什么？
答：DE与BC
 

理由如下：∵CD⊥AB，FG⊥AB（　　）
∴∠BGF=
 
=90°（　　）
∴GF∥DC（　　）
又∠BDC+∠DCB+∠B=180°（　　）
∠BGF+∠1+∠B=180°（　　）
∴∠1=
 
（　　）
又∠1=∠2（　　）
∴∠2=
 
（　　）
∴
 
∥
 
（　　）
如图，已知PE∥AB，PE交BC于E，PF∥CB，PF交BA于F，PH⊥BA，垂足为点H，∠CEP=43°，求∠FPH的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网