题目内容
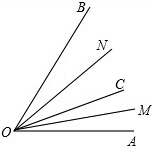 如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线
如图所示,OM是∠AOC的平分线,ON是∠BOC的平分线(1)如果∠MON=30°,求出∠AOB的度数;
(2)如果∠MON=50°,求出∠AOB的度数;
(3)如果∠MON的大小改变,∠AOB的大小是否随之改变?它们之间有怎样的大小关系?请写出来.
考点:角平分线的定义
专题:
分析:(1)、(2)根据角平分线的定义,用∠NOC表示出∠BOC,用∠COM表示出∠AOC,然后即可得解;
(3)根据(2)的推导得解.
(3)根据(2)的推导得解.
解答:
解:(1)∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠COM=
∠AOC,∠CON=
∠BOC,
∴∠MON=∠COM+∠CON=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
∠AOB,
∵∠MON=30°,
∴∠AOB=2∠MON=70°;
(2)∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠COM=
∠AOC,∠CON=
∠BOC,
∴∠MON=∠COM+∠CON=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
∠AOB,
∵∠MON=50°,
∴∠AOB=2∠MON=100°;
(3)根据(2)的推导,∠AOB随∠MON大小的改变而改变,∠AOB=2∠MON.
∴∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠COM+∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠MON=30°,
∴∠AOB=2∠MON=70°;
(2)∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠COM+∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠MON=50°,
∴∠AOB=2∠MON=100°;
(3)根据(2)的推导,∠AOB随∠MON大小的改变而改变,∠AOB=2∠MON.
点评:本题考查了角平分线的定义以及角的计算,熟记角平分线的定义是解题的关键.

练习册系列答案
相关题目
已知二次函数y=kx2-2x-1(k≠0)的图象与x轴有两个交点,则k的取值范围是( )
| A、k>-1且k≠0 |
| B、k>-1 |
| C、k<1且k≠0 |
| D、k<1 |
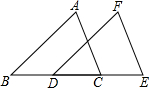 如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.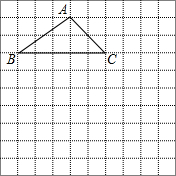 如图所示,在10×10正方形网格中,△ABC的三个顶点都在格点上,请按下列要求画图并回答问题:
如图所示,在10×10正方形网格中,△ABC的三个顶点都在格点上,请按下列要求画图并回答问题: 如图,已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x,沿y轴向上平移,分别交x轴,y轴于C、D两点.CD⊥CP,且CD=2CP,求点P的坐标.
如图,已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x,沿y轴向上平移,分别交x轴,y轴于C、D两点.CD⊥CP,且CD=2CP,求点P的坐标.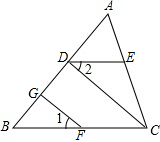 如图,在△ABC中,CD⊥AB于点D,FG⊥AB于点G,∠1=∠2,问DE与BC的关系如何,为什么?
如图,在△ABC中,CD⊥AB于点D,FG⊥AB于点G,∠1=∠2,问DE与BC的关系如何,为什么?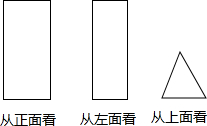 已知如图是三个方向看到的一个几何体的形状.
已知如图是三个方向看到的一个几何体的形状. 如图,在⊙O中,OA是半径,AB,AC是弦,且
如图,在⊙O中,OA是半径,AB,AC是弦,且