题目内容
12.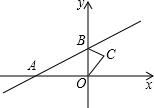 如图,直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-8,-3)或(4,3).
如图,直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为(-8,-3)或(4,3).
分析 首先解得点A和点B的坐标,再利用位似变换可得结果.
解答 解:∵直线y=$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,
令x=0可得y=1;
令y=0可得x=-2,
∴点A和点B的坐标分别为(-2,0);(0,1),
∵△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,
∴$\frac{OB}{O′B′}$=$\frac{OA}{AO′}$=$\frac{1}{3}$,
∴O′B′=3,AO′=6,
∴B′的坐标为(-8,-3)或(4,3).
故答案为:(-8,-3)或(4,3).
点评 本题主要考查了位似变换和一次函数图象上点的坐标特征,得出点A和点B的坐标是解答此题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
2.下列说法正确的是( )
| A. | 抛一枚图钉钉尖着地和钉尖朝上的概率一样大 | |
| B. | 彩票中奖的机会是1%,买100张一定会中奖 | |
| C. | 天气预报说明天下雨的概率是50%,所以明天将有一半的时间在下雨 | |
| D. | 在同一年出生的367名学生中,至少有两人的生日是同一天 |
20. 如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )
 如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )| A. | 58° | B. | 90° | C. | 32° | D. | 38° |
4. 某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率分布表
根据以上图表信息,解答下列问题:
(1)表中a=12,b=0.08;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
 某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:参加社区活动次数的频数、频率分布表
| 活动次数x | 频数 | 频率 |
| 0<x≤3 | 10 | 0.20 |
| 3<x≤6 | a | 0.24 |
| 6<x≤9 | 16 | 0.32 |
| 9<x≤12 | 6 | 0.12 |
| 12<x≤15 | m | b |
| 15<x≤18 | 2 | n |
(1)表中a=12,b=0.08;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
1. 在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )
在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )
 在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )
在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )| A. | 2$\sqrt{3}$-$\frac{2}{3}$π | B. | 4$\sqrt{3}$-$\frac{2}{3}$π | C. | 2$\sqrt{3}$-$\frac{4}{3}$π | D. | $\frac{2}{3}$π |
2.设α、β是一元二次方程x2+2x-1=0的两个根,则αβ的值是( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
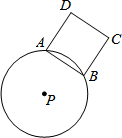 如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π.
如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π.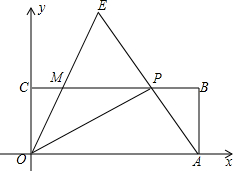 如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.