题目内容
3.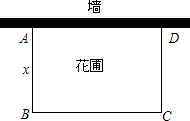 如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m).设花圃的面积为ym2,AB的长为xm.
如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m).设花圃的面积为ym2,AB的长为xm.(1)求y与x的函数关系式,并写出x的取值范围.
(2)x为何值时,y取得最大值?最大值是多少?
分析 (1)AB的长为xm,则平行于墙的一边长为(24-3x)m,该花圃的面积为[(24-x)x]m;进而得出函数关系即可;
(2)根据二次函数的性质即可求出最大值.
解答 解:(1)S=(24-2x)x=24x-2x2;
又∵x>0,且20≥24-2x>0,
∴2≤x<12;
(2)S=-2x2+24x=-2(x-6)2+72,
∵-2<0,对称轴x=6,
∴当x>6时,y随x的增大而减小,
∴当x=6时,y的值最大,最大值y=72.
点评 本题主要考查了二次函数的实际应用,根据题目的条件,合理地建立函数关系式,利用函数的性质解决问题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
14.下列具有相反意义的量的是( )
| A. | 上升1米与下降2℃ | B. | 盈利2万元与亏损3万元 | ||
| C. | 气温升高3℃与气温为-3℃ | D. | 体重增加与体重减少 |
18.数轴上点M表示有理数-3,将点M向右平移2个单位长度到达点N,点E到点N的距离为4,则点E表示的有理数为( )
| A. | 3 | B. | -5或3 | C. | -9或-1 | D. | -1 |
8. 在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
(1)求这个二次函数的解析式及m的值;
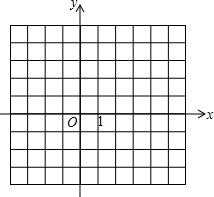
(2)在平面直角坐标系中,用描点法画出这个二次函数的图象(不用列表);
(3)当y<3时,则x的取值范围是0<x<4.
 在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | m | … |
(2)在平面直角坐标系中,用描点法画出这个二次函数的图象(不用列表);
(3)当y<3时,则x的取值范围是0<x<4.
15.等腰三角形一腰上的高与另一腰的夹角是28°,则顶角是( )
| A. | 28° | B. | 118° | C. | 62° | D. | 62°或118° |
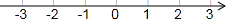 (1)解不等式2(x+1)-1≥3x+2.并把它的解集在数轴上表示出来.
(1)解不等式2(x+1)-1≥3x+2.并把它的解集在数轴上表示出来.