题目内容
8. 在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:
在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如表:| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | m | … |
(2)在平面直角坐标系中,用描点法画出这个二次函数的图象(不用列表);
(3)当y<3时,则x的取值范围是0<x<4.
分析 (1)由二次函数图象经过点(1,0),(3,0),设出交点式,利用待定系数法求函数解析式,进一步代入点得出答案即可;
(2)利用表中的点描点,画出函数图象即可;
(3)利用图象得出答案即可.
解答 解:(1)∵抛物线y=ax2+bx+c(a≠0)过点(1,0),(3,0),
∴可设抛物线解析式为y=a(x-1)(x-3),
∵过点(0,3),
∴a=1,
∴y=(x-1)(x-3)=x2-4x+3,
当x=4时,m=3,
∴抛物线的解析式为y=x2-4x+3,m的值为3.
(2)y=x2-4x+3=(x-2)2-1,
顶点坐标为(2,-1),与y轴的交点坐标为(0,3),
函数图象如下:
(3)由图表可知抛物线y=ax2+bx+c过点(0,3),(4,3),
因此当y<3时,x的取值范围是0<x<4.
点评 此题考查待定系数法求函数解析式,二次函数的图象,掌握待定系数法求函数解析式的方法与步骤是解决问题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
17.下列语句中,不是命题的是( )
| A. | 直角都相等 | B. | 正数大于0 | C. | 作线段AB=CD | D. | -4>5 |
18.若x=1时,式子ax3+bx+4=-5,那么x=-1时,多项式ax3+bx-3的值是( )
| A. | -2 | B. | 6 | C. | 12 | D. | -12 |
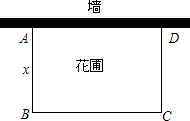 如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m).设花圃的面积为ym2,AB的长为xm.
如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m).设花圃的面积为ym2,AB的长为xm. 如图,已知这是一座圆弧形涵洞的入口的示意图,涵洞的最高点C到地面AB的距离为6米,涵洞入口地面的宽度AB为4米,请你求这座涵洞圆弧所在圆的半径长.
如图,已知这是一座圆弧形涵洞的入口的示意图,涵洞的最高点C到地面AB的距离为6米,涵洞入口地面的宽度AB为4米,请你求这座涵洞圆弧所在圆的半径长. 如图,抛物线y=ax2+bx+c请根据图象写出该图象两条性质:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大..
如图,抛物线y=ax2+bx+c请根据图象写出该图象两条性质:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大..