题目内容
11.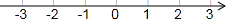 (1)解不等式2(x+1)-1≥3x+2.并把它的解集在数轴上表示出来.
(1)解不等式2(x+1)-1≥3x+2.并把它的解集在数轴上表示出来.(2)解不等式组:$\left\{\begin{array}{l}{3x>x-2}\\{\frac{x+1}{3}>2x}\end{array}\right.$,并写出该不等式组的整数解.
分析 (1)不等式去括号,移项合并,把x系数化为1,求出解集,表示在数轴上即可;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出整数解即可.
解答 解:(1)去括号得:2x+2-1≥3x+2,
解得:x≤-1,
如图所示:
(2)$\left\{\begin{array}{l}{3x>x-2①}\\{\frac{x+1}{3}>2x②}\end{array}\right.$,
由①得:x>-1,
由②得:x<0.2,
则不等式组的解集为-1<x<0.2,
则方程组的整数解为x=0.
点评 此题考查了解一元一次不等式组,以及在数轴上表示不等式的解集,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
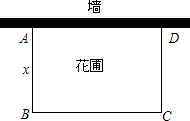 如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m).设花圃的面积为ym2,AB的长为xm.
如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m).设花圃的面积为ym2,AB的长为xm. 如图,抛物线y=ax2+bx+c请根据图象写出该图象两条性质:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大..
如图,抛物线y=ax2+bx+c请根据图象写出该图象两条性质:①开口方向向下;②对称轴x=1,当x>1时,y随着x的增大而减小,当x<1时,y随着x的增大而增大..