Question

10．如图，网格中每个小正方形的边行均为1，线段AB，线段CD的端点均在小正方形的顶点上．
（1）在图中画以AB为直角边的等腰直角△ABE，顶点E在小正方形的顶点上；
（2）在（1）的条件下，在图中以CD为边画直角△CDF，点F在小正方形的顶点上，使∠CDF=90°，且△CDF的面积为6，连接DE，直接写出∠EDF的正切值．

Answer 1

分析 （1）根据条件画出△ABE，使得∠ABE=90°，AB=BE即可．
（2）根据条件画出△CDF，使得∠CDF=90°，DF=3$\sqrt{2}$即可，在Rt△根据tan∠EDF=$\frac{EF}{DF}$，计算即可解决问题．

解答 解：（1）以AB为直角边的等腰直角△ABE如图所示，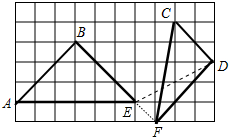

（2）以CD为边画直角△CDF，点F在小正方形的顶点上，使∠CDF=90°，且△CDF的面积为6，△CDF如图所示．
在Rt△DEF中，tan∠EDF=$\frac{EF}{DF}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$．

点评 本题考查等腰直角三角形的性质、勾股定理．三角形的面积、锐角三角函数等知识，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．