Question

5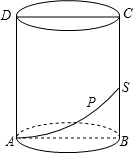．如图，圆柱的轴截面ABCD，是边长为4的正方形，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$．

Answer 1

分析 由于圆柱底面直径AB、母线BC均为4cm，S为BC的中点，故BS=2cm，先把圆柱的侧面展开，连接AS，利用勾股定理即可得出AS的长．

解答 解：∵圆柱底面直径AB、母线BC均为4，S为BC的中点，
∴圆柱底面圆的半径是2，BS=2，
如图所示：
连接AS，在Rt△ABS中，AS=$\sqrt{A{B}^{2}+B{S}^{2}}$=2$\sqrt{1+{π}^{2}}$．
故答案为：2$\sqrt{1+{π}^{2}}$．

点评 本题考查的是平面展开-最短路径问题，根据题意画出圆柱的侧面展开图，利用勾股定理求解是解答此题的关键．