题目内容
15.如果方程x2+px+q=0有两个实数根x1,x2,那么x1+x2=-p,x1x2=q,请根据以上结论,解决下列问题:(1)已知a、b是方程x2+15x+5=0的二根,则$\frac{a}{b}+\frac{b}{a}$=43
(2)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值.
(3)结合二元一次方程组的相关知识,解决问题:已知$\left\{\begin{array}{l}x={x_1}\\ y={y_1}\end{array}$和$\left\{\begin{array}{l}x={x_2}\\ y={y_2}\end{array}$是关于x,y的方程组$\left\{\begin{array}{l}{x^2}-y+k=0\\ x-y=1\end{array}$的两个不相等的实数解.问:是否存在实数k,使得y1y2-$\frac{x_1}{x_2}-\frac{x_2}{x_1}$=2?若存在,求出的k值,若不存在,请说明理由.
分析 (1)根据a,b是x2+15x+5=0的解,求出a+b和ab的值,即可求出$\frac{a}{b}+\frac{b}{a}$的值.
(2)根据a+b+c=0,abc=16,得出a+b=-c,ab=$\frac{16}{c}$,a、b是方程x2+cx+$\frac{16}{c}$=0的解,再根据c2-4•$\frac{16}{c}$≥0,即可求出c的最小值.
(3)运用根与系数的关系求出x1+x2=1,x1•x2=k+1,再解y1y2-$\frac{x_1}{x_2}-\frac{x_2}{x_1}$=2,即可求出k的值.
解答 解:(1)∵a、b是方程x2+15x+5=0的二根,
∴a+b=-15,ab=5,
∴$\frac{a}{b}+\frac{b}{a}$=$\frac{(a+b)^{2}-2ab}{ab}$=$\frac{(-1{5)}^{2}-2×5}{5}$=43,
故答案是:43;
(2)∵a+b+c=0,abc=16,
∴a+b=-c,ab=$\frac{16}{c}$,
∴a、b是方程x2+cx+$\frac{16}{c}$=0的解,
∴c2-4•$\frac{16}{c}$≥0,c2-$\frac{{4}^{3}}{c}$≥0,
∵c是正数,
∴c3-43≥0,c3≥43,c≥4,
∴正数c的最小值是4.
(3)存在,当k=-2时,${y_1}{y_2}-\frac{x_1}{x_2}-\frac{x_2}{x_1}=2$.
由x2-y+k=0变形得:y=x2+k,
由x-y=1变形得:y=x-1,把y=x-1代入y=x2+k,并整理得:x2-x+k+1=0,
由题意思可知,x1,x2是方程x2-x+k+1=0的两个不相等的实数根,故有:
$\left\{\begin{array}{l}{(-1)^2}-4(k+1)>0\\{x_1}+{x_2}=1\\{x_1}{x_2}=k+1\\{y_1}{y_2}=({x_1}-1)({x_2}-1)\\{y_1}{y_2}-\frac{x_1}{x_2}-\frac{x_2}{x_1}=({x_1}-1)({x_2}-1)-\frac{{{{({x_1}+{x_2})}^2}-2{x_1}{x_2}}}{{{x_1}{x_2}}}=2\end{array}\right.$
即:$\left\{\begin{array}{l}k<-\frac{3}{4}\\{k^2}+2k=0\end{array}\right.$
解得:k=-2.
点评 本题考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

| A. |  | B. |  | C. |  | D. |  |
| A. | -2(x-2)=12 | B. | -2(x-1)=4 | C. | 11x+1=5(2x+1) | D. | 2-(1-x)=-2 |
| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 5元 | 4.5元 | 4元 |
(1)如果两班合起来,作为一个团体购票,可以节约多少钱?
(2)两班各有多少学生?
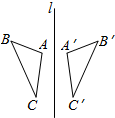 如图,△ABC与△A′B′C′关于直线l对称,且∠A=98°,∠C′=48°,则∠B的度数为34°.
如图,△ABC与△A′B′C′关于直线l对称,且∠A=98°,∠C′=48°,则∠B的度数为34°.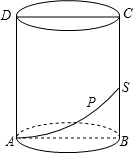 如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.
如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.