题目内容
13. 中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 过点C作CD垂直AB延长线于点D,设CD为x米,在Rt△ACD和Rt△BCD中,分别表示出AD和BD的长度,然后根据AB=2000米,求出x的值,求出点C距离海面的距离,判断是否在极限范围内;
解答  解:(1)过点C作CD垂直AB延长线于点D,
解:(1)过点C作CD垂直AB延长线于点D,
设CD=x米,
在Rt△ACD中,
∵∠DAC=45°,
∴AD=x,
在Rt△BCD中,
∵∠CBD=60°,
∴BD=$\frac{\sqrt{3}}{3}$x,
∴AB=AD-BD=x-$\frac{\sqrt{3}}{3}$x=2000,
解得:x≈4732,
∴船C距离海平面为4732+1800=6532米<7062.68米,
∴沉船C在“蛟龙”号深潜极限范围内.
点评 本题考查了解直角三角形的应用,解答本题的关键是利用俯角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
相关题目
4.暑假期间某风景区推出优惠措施如下表:
七年级(1)班和(2)班共103人(其中(1)班人数多于(2)班人数)去该风景区参观,如果以班为单位购票,两班共需付486元.问:
(1)如果两班合起来,作为一个团体购票,可以节约多少钱?
(2)两班各有多少学生?
| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 5元 | 4.5元 | 4元 |
(1)如果两班合起来,作为一个团体购票,可以节约多少钱?
(2)两班各有多少学生?
2.平方得4的数是( )
| A. | +2 | B. | -2 | C. | ±4 | D. | ±2 |
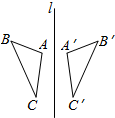 如图,△ABC与△A′B′C′关于直线l对称,且∠A=98°,∠C′=48°,则∠B的度数为34°.
如图,△ABC与△A′B′C′关于直线l对称,且∠A=98°,∠C′=48°,则∠B的度数为34°. 有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|-|c-b|-|b+a|=2b-2c.
有理数a,b,c表示的点在数轴上的位置如图所示,则|a+c|-|c-b|-|b+a|=2b-2c.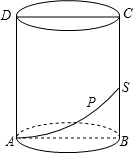 如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.
如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.