题目内容
17.已知一口袋中放有红、白、黑三种颜色的球共50个,它们除颜色外其他都一样,一位同学通过多次试验后发现摸到红、白色的频率基本稳定是45%和15%,则袋中黑球的个数可能是( )| A. | 16 | B. | 18 | C. | 20 | D. | 22 |
分析 由于通过多次试验后发现其中摸到红色、白色的频率基本稳定在45%和15%,由此可以确定摸到袋中黑球的概率,然后就可以求出袋中黑球的个数.
解答 解:∵通过多次试验后发现其中摸到红色、白色的频率基本稳定在45%和15%,
∴摸到袋中黑球的概率为1-45%-15%=40%,
∴袋中黑球的个数为50×40%=20.
故选C.
点评 此题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.

练习册系列答案
相关题目
12.阅读理解题:
如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
(1)可求得x=9,第2015个格子中的数为-6;
(2)判断:前n个格子中所填整数之和是否可能为2015?若能,求出n的值,若不能,请说明理由;
(3)若取前3格子中的任意两个数,记作a、b,且a≥b,那么所有的|a-b|的和可以通过计算|9-★|+|9-☆|+|☆-★|得到.其结果为30;若取前19格子中的任意两个数,记作s、t,且s≥t,求所有的|s-t|的和.
如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
| 9 | ★ | ☆ | x | -6 | 2 | … |
(2)判断:前n个格子中所填整数之和是否可能为2015?若能,求出n的值,若不能,请说明理由;
(3)若取前3格子中的任意两个数,记作a、b,且a≥b,那么所有的|a-b|的和可以通过计算|9-★|+|9-☆|+|☆-★|得到.其结果为30;若取前19格子中的任意两个数,记作s、t,且s≥t,求所有的|s-t|的和.
2.平方得4的数是( )
| A. | +2 | B. | -2 | C. | ±4 | D. | ±2 |
7.解方程(x-2015)2=1得方程的根为( )
| A. | 2018 | B. | 2014或2016 | C. | 2017或1 | D. | 2016或0 |
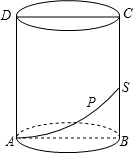 如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.
如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.