题目内容
14.求值:(1)已知a=$\frac{1}{2}$,b=$\frac{1}{4}$,求$\frac{{\sqrt{b}}}{{\sqrt{a}-\sqrt{b}}}$-$\frac{{\sqrt{b}}}{{\sqrt{a}+\sqrt{b}}}$的值.
(2)已知x=$\frac{1}{{\sqrt{5}-2}}$,求x2-x+$\sqrt{5}$的值.
分析 (1)根据通分法则计算;
(2)把x的值进行分母有理化化简,根据完全平方公式计算即可.
解答 解:(1)原式=$\frac{{\sqrt{b}(\sqrt{a}+\sqrt{b})-\sqrt{b}(\sqrt{a}-\sqrt{b})}}{{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}}$
=$\frac{{\sqrt{ab}+b-\sqrt{ab}+b}}{a-b}$
=$\frac{2b}{a-b}$.
当a=$\frac{1}{2}$,b=$\frac{1}{4}$时,
原式=$\frac{{2×\frac{1}{4}}}{{\frac{1}{2}-\frac{1}{4}}}$=2.
2)∵x=$\frac{1}{{\sqrt{5}-2}}$=$\frac{{\sqrt{5}+2}}{5-4}$=$\sqrt{5}+2$.
∴x2-x+$\sqrt{5}$=($\sqrt{5}$+2)2-($\sqrt{5}$+2)+$\sqrt{5}$
=5+4$\sqrt{5}$+4-$\sqrt{5}$-2+$\sqrt{5}$
=7+4$\sqrt{5}$.
点评 本题考查的是二次根式的化简求值,掌握二次根式的性质、完全平方公式以及有理数的运算法则是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.暑假期间某风景区推出优惠措施如下表:
七年级(1)班和(2)班共103人(其中(1)班人数多于(2)班人数)去该风景区参观,如果以班为单位购票,两班共需付486元.问:
(1)如果两班合起来,作为一个团体购票,可以节约多少钱?
(2)两班各有多少学生?
| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 5元 | 4.5元 | 4元 |
(1)如果两班合起来,作为一个团体购票,可以节约多少钱?
(2)两班各有多少学生?
2.平方得4的数是( )
| A. | +2 | B. | -2 | C. | ±4 | D. | ±2 |
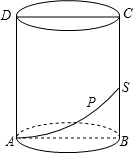 如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.
如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.