题目内容
20.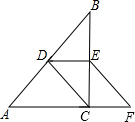 在Rt△ABC中,∠ACB=90°,D、E分别为边AB、BC的中点,点F在边AC的延长线上,∠FEC=∠B,求证:四边形CDEF是平行四边形.
在Rt△ABC中,∠ACB=90°,D、E分别为边AB、BC的中点,点F在边AC的延长线上,∠FEC=∠B,求证:四边形CDEF是平行四边形.
分析 由三角形中位线定理得出DE∥AC,由直角三角形斜边上的中线性质得出CD=$\frac{1}{2}$AB=AD=BD,由等腰三角形的性质得出∠B=∠DCE,证出∠FEC=∠DCE,得出DC∥EF,即可证出四边形CDEF是平行四边形.
解答 证明:∵ 在Rt△ABC中,∠ACB=90°,D、E分别为边AB、BC的中点,
在Rt△ABC中,∠ACB=90°,D、E分别为边AB、BC的中点,
∴DE∥AC,CD=$\frac{1}{2}$AB=AD=BD,
∴∠B=∠DCE,
∵∠FEC=∠B,
∴∠FEC=∠DCE,
∴DC∥EF,
∴四边形CDEF是平行四边形.
点评 本题考查了平行四边形的判定、三角形中位线定理、直角三角形斜边上的中线性质、等腰三角形的性质、平行线的判定;熟练掌握平行四边形的判定方法,证明DC∥EF是解决问题的关键.

练习册系列答案
相关题目
8.已知正六边形ABCDEF的边心距为$\sqrt{3}$cm,则正六边形的半径为( )cm.
| A. | 2$\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
10.已知平行四边形ABCD中,∠A=2∠B,则∠C=( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
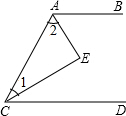 如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.试说明CD∥AB.
如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.试说明CD∥AB.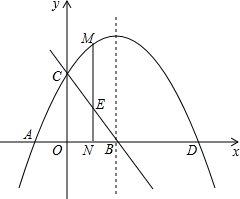 如图,抛物线y=ax2+bx+4与x轴交于A(-2,0),D两点,与y轴交于点C,对称轴x=3交x轴交于点B.
如图,抛物线y=ax2+bx+4与x轴交于A(-2,0),D两点,与y轴交于点C,对称轴x=3交x轴交于点B.