题目内容

8．用配方法解下列一元二次方程：
（1）x2-6x-4=0
（2）a2-4a-7=0．

分析 （1）移项后配方，再开方，即可得出两个一元一次方程，求出方程的解即可；
（2）移项后配方，再开方，即可得出两个一元一次方程，求出方程的解即可．

解答 解：（1）x2-6x-4=0，
x2-6x=4，
x2-6x+9=9+4，
（x-3）2=13，
x-3=±$\sqrt{13}$，
解得：x1=3+$\sqrt{13}$，x2=3-$\sqrt{13}$；
（2）a2-4a-7=0，
a2-4a=7，
a2-4a+4=7+4，
（a-2）2=11，
a-2=±$\sqrt{11}$，
解得：a1=2+$\sqrt{11}$，a2=2-$\sqrt{11}$．

点评 本题考查利用配方法解一元二次方程，解此题的关键是能正确配方，掌握解答的步骤与方法．

练习册系列答案
相关题目
18．在平面直角坐标系中，已知点A（1，0），B（1-$\sqrt{2}$，$\sqrt{2}$），以AB为边作正方形ABCD，则该正方形的对角线交点坐标是（1，$\sqrt{2}$）或（1-$\sqrt{2}$，0）．
19．方程x2-4x-m2=0根的情况是（　　）
A．一定有两不等实数根B．一定有两相等实数根
C．一定无实数根D．根的情况不确定
16．观察下列各式，请你找出规律回答以下问题：
2=2×1
2+4=6=2×3
2+4+6=12=3×4
2+4+6+8=20=4×5
…
计算：
（1）2+4+6+8+10+…+20=110
（2）2+4+6+8+10+…+2×n=n（n+1）
（3）30+32+34+36+…+200=9890．
3．在$\sqrt{8}$，-$\sqrt{4}$，$\root{3}{-27}$，0，$\frac{π}{2}$，3$\frac{1}{7}$，3.1415，0.2020020002…，1.4142各数中，无理数$\sqrt{8}$，$\frac{π}{2}$，0.2020020002…（全部写出）
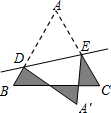13．如图，等边三角形ABC的边长为1cm，DE分别是AB、AC上的点，将△ABC沿直线DE折叠，点A落在点A′处，在△ABC外部，则阴影部分的周长为3cm．
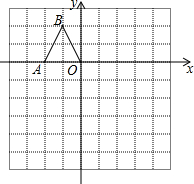20．若关于x的方程$\frac{x-2}{x-3}=\frac{m}{x-3}+2$无解，则m的值为（　　）
A．1B．-1C．0D．3
17．如图，在边长均为1的小正方形网格纸中，△OAB的顶点O、A、B均在格点上，且O是直角坐标系的原点，点A在x轴上．
（1）以O为位似中心，将△OAB放大，使得放大后的△OA1B1与△OAB对应线段的比为2：1，画出△OA1B1 （所画△OA1B1与△OAB在位似中心两侧）．
（2）直接写出线段A1B1的长为2$\sqrt{5}$；
（3）在（1）的条件下，若△OAB内一点P（x，y）与△OA1B1内一点P′是一对对应点，则点P′的坐标是（-2x，-2y）．
18．已知点A（3，2）与点B（x，3x+1）在同一条垂直于x轴的直线上，且C是线段AB的中点，试写出点B、点C的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网