题目内容
13．
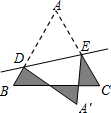如图，等边三角形ABC的边长为1cm，DE分别是AB、AC上的点，将△ABC沿直线DE折叠，点A落在点A′处，在△ABC外部，则阴影部分的周长为3cm．
分析 根据翻折的性质可得A′D=AD，A′E=AE，然后求出阴影部分的周长等于△ABC的周长，再根据等边三角形的性质求解即可．
解答 解：∵△ABC沿直线DE折叠，点A落在点A′处，
∴A′D=AD，A′E=AE，
∴阴影部分的周长=A′D+BD+A′E+CE+BC=AB+AC+BC=△ABC的周长，
∵△ABC的边长为1cm的等边三角形，
∴阴影部分的周长=3×1=3cm．
故答案为：3cm．
点评 本题考查了翻折变换，等边三角形的性质，熟记翻折前后的图形的对应边相等是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
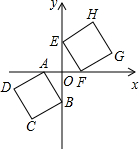如图，边长均为3的正方ABCD与正方形EFGH在平面直角坐标系中关于原点对称，点A（-1，0）．
请根据图中“X”与“Y”的话语，解答下列各小题．