题目内容
4.当-1≤x≤2时,关于x的二次函数y=(x-m)2-m2+1有最小值-2,则实数m的值为$\sqrt{3}$或-2.分析 根据二次函数的最值问题列出方程求出m的值,再根据二次项系数大于0解答.
解答 解:∵关于x的二次函数y=(x-m)2-m2+1有最小值-2,
二次项系数a=1>0,故图象开口向上,对称轴为x=m,
当m<-1时,最小值在x=-1取得,此时有(m+1)2+1-m2=-2,
求得m=-2,符合m<-1;
当-1≤m≤2时,最小值在x=m时取得,即有1-m2=-2
求得m=$\sqrt{3}$或m=-$\sqrt{3}$(舍去)
当m>2时,最小值在x=2时取得,即(2-m)2-m2+1=-2
求得m=$\frac{7}{4}$(舍去)
故答案为:$\sqrt{3}$或-2.
点评 本题考查了二次函数的最值问题,要注意二次函数有最小值,二次项系数大于0.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
15.用棋子按下列方式摆图形,依照此规律,第n个图形比第(n-1)个图形多( )


| A. | (n-1)枚棋子 | B. | n枚棋子 | C. | (n+1)枚棋子 | D. | (3n-2)枚棋子 |
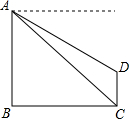 小明在电视塔上高度为450米的A处,测得大楼CD楼顶D的俯角30°,小杰在大楼楼底C处测得A处的仰角为45°.
小明在电视塔上高度为450米的A处,测得大楼CD楼顶D的俯角30°,小杰在大楼楼底C处测得A处的仰角为45°. 已知实数a,b,c在数轴上所对应的点如图所示,完成下列各题.
已知实数a,b,c在数轴上所对应的点如图所示,完成下列各题.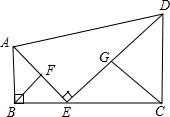 如图所示,梯形ABCD中,AB∥CD,∠ABE=90°,BFCG分别是△ABE和△ECD的中线,E为BC上一点,且AE⊥ED,若BC=DC=8,BE:EC=1:1,CG=2$\sqrt{5}$,求BF的长.
如图所示,梯形ABCD中,AB∥CD,∠ABE=90°,BFCG分别是△ABE和△ECD的中线,E为BC上一点,且AE⊥ED,若BC=DC=8,BE:EC=1:1,CG=2$\sqrt{5}$,求BF的长. 已知:如图,在△ABC中,∠C=90°,AC=4,CB=5,D是BC边上一点,且DB=2,点E是AC边上的一个动点,过点E作EF∥CB交AD于点F.
已知:如图,在△ABC中,∠C=90°,AC=4,CB=5,D是BC边上一点,且DB=2,点E是AC边上的一个动点,过点E作EF∥CB交AD于点F. 如图,木匠小王想从对角线长为80cm的正方形木板上截下一个最大的洞,试求这个圆的直径是多少?
如图,木匠小王想从对角线长为80cm的正方形木板上截下一个最大的洞,试求这个圆的直径是多少?