题目内容
13.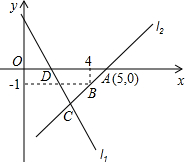 如图,直线l1的表达式为y=-2x+4,且l1与x轴交于点D,直线l2经过点A,B,点A的坐标为(5,0),直线l1,l2交于点C.
如图,直线l1的表达式为y=-2x+4,且l1与x轴交于点D,直线l2经过点A,B,点A的坐标为(5,0),直线l1,l2交于点C.(1)求直线l2的函数表达式;
(2)求△ADC的面积;
(3)在直线l2上有一点P,且S△ADP=2S△ADC,请直接写出点P的坐标.
分析 (1)利用待定系数法求出一次函数解析式即可;
(2)利用y=0,求出x的值,即可得出D点坐标,进一步利用三角形的面积计算方法求得答案即可;
(3)利用S△ADP=2S△ADC,得出点P的纵坐标是点C的纵坐标的2倍,即可求出答案即可.
解答 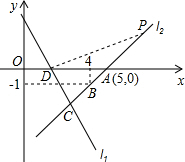 解:(1)设l2的解析式为:y=kx+b,
解:(1)设l2的解析式为:y=kx+b,
由图象可知:$\left\{\begin{array}{l}{5k+b=0}\\{4k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=5}\end{array}\right.$,
∴直线l2的解析式为:y=x-5;
(2)对于函数:y=-2x+4,令y=0,
∴-2x+4=0,
x=2,
即D点坐标为:(2,0),
直线l1,l2交于点C,
则$\left\{\begin{array}{l}{y=-2x+4}\\{y=x-5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$
点C为(3,-2)
△ADC的面积=$\frac{1}{2}$×(5-2)×2=3.
(3)直线l2上存在点P使得S△ADP=2S△ADC,
∵S△ADP=2S△ADC,C(3,-2),
∴点P的纵坐标是点C的纵坐标的2倍,
∴x-5=±4,
∴x=9或1,
∴y=4或-4
即P点坐标为:(9,4),(1,-4).
点评 此题主要考查了一次函数的综合应用以及待定系数法求一次函数解析式,三角形的面积,根据已知结合图形得出点P的纵坐标与点C的纵坐标之间的关系是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
4.某通讯公司推出移动电话的两种计费方式(详请见下表)
温馨提示:若选用方式一,每月固定交费58元,当主动打出电话月累计时间不超过150分,不再额外交费;当超过150分,超过部分加收0.25元.
设一个月内使用移动电话主叫的时间为t分(t为正整数),
请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
(2)当t=270时,哪种计费方式更省钱?请通过计算说明你的理由.
(3)当t>350时,请选择哪一种说法最合理B
A.方式一计费省钱 B.方式二计费省钱
C.两种方式计费相同 D.无法判定.
| 固定交费 | 主叫限定 时间/分 | 主叫超时费 (元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
设一个月内使用移动电话主叫的时间为t分(t为正整数),
请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
| t≤150 | 150<t<350 | t=350 | t>350 | |
| 方式一计费/元 | 58 | 0.25t+20.5 | 108 | 0.25t+20.5 |
| 方式二计费/元 | 88 | 88 | 88 | 0.19t+21.5 |
(3)当t>350时,请选择哪一种说法最合理B
A.方式一计费省钱 B.方式二计费省钱
C.两种方式计费相同 D.无法判定.
1.已知反比例函数y=$\frac{k}{x}$(k≠0)的图象,在每一个象限内,y随x的增大而增大,则一次函数y=-kx+k的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.若一次函数y=(1-m)x|m|-1+3的函数值y随x的增大而增大,则m的取值为( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
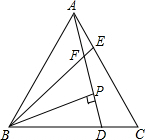 如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.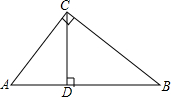 如图,已知Rt△ABC,∠C=90°,CD是斜边AB上的高.
如图,已知Rt△ABC,∠C=90°,CD是斜边AB上的高.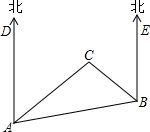 如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?
如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?