题目内容
20．从-2，0，$\sqrt{5}$，π，（-2）-1中随机任取一数，取到无理数的概率是$\frac{2}{5}$．分析 先找出无理数的个数，再根据概率公式进行求解即可．
解答 解：在-2，0，$\sqrt{5}$，π，（-2）-1中，无理数有$\sqrt{5}$，π，共2个，
则取到无理数的概率是$\frac{2}{5}$；
故答案为：$\frac{2}{5}$．
点评 此题考查了概率公式，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
已知：如图，FA⊥AC，EB⊥AC，垂足分别为A、B，且∠BED+∠D=180°，求证：AF∥CD．
11．“十一”黄金周期间，某市在7天中外出旅游的人数变化如表（正数表示比前一天多的人数，负数表示比前一天少的人数（单位：万人）
（1）若9月30日外出旅游人数记为m，请用含m的代数式表示10月3日外出旅游的人数．
（2）请判断七天内外出旅游人数最多的是哪天？最少的是哪天？它们相差多少万人．
（3）如果最多一天有出游人数5万人，问9月30日出去旅游的人数有多少？
| 日期 | 10月1 | 10月2 | 10月3 | 10月4 | 10月5 | 10月6 | 10月7 |
| 人数变化 | +1.5 | +0.7 | +0.3 | +0.4 | -0.6 | +0.2 | -1.3 |
（2）请判断七天内外出旅游人数最多的是哪天？最少的是哪天？它们相差多少万人．
（3）如果最多一天有出游人数5万人，问9月30日出去旅游的人数有多少？
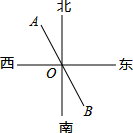如图，已知点A、O、B在同一条直线上，若OA的方向是北偏西28°，则OB的方向是南偏东28°．
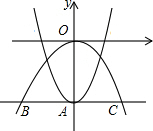如图，抛物线y=ax2-2与y轴交于点A，过点A与x轴平行的直线交抛物线y=-$\frac{1}{2}$x2于点B，C，则S△BOC=4．
5．若点P（a，2015）与点Q（2016，b）关于x轴对称，则（a+b）2016的值是（ ）
| A． | 1 | B． | -1 | C． | 2016 | D． | 40312016 |
如图，边长为2的菱形ABCD中，BD=2，E、F分别是AD，CD上的动点（包含端点），且AE+CF=2，则线段EF长的取值范围是$\sqrt{3}$≤EF≤2．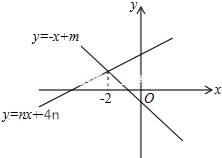
如图，直线y1=-x+m与y2=nx+4n（n≠0）的交点的横坐标为-2，图象可得关于x的不等式组$\left\{\begin{array}{l}{-x+m＞nx+4n}\\{nx+4n＞0}\end{array}\right.$的解集为-4＜x＜-2．