题目内容
15.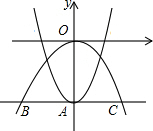 如图,抛物线y=ax2-2与y轴交于点A,过点A与x轴平行的直线交抛物线y=-$\frac{1}{2}$x2于点B,C,则S△BOC=4.
如图,抛物线y=ax2-2与y轴交于点A,过点A与x轴平行的直线交抛物线y=-$\frac{1}{2}$x2于点B,C,则S△BOC=4.
分析 根据抛物线与y轴相交,求出点A的坐标,令y=-2时,求出点B,C的坐标,根据三角形的面积公式即可解答.
解答 解:∵抛物线y=ax2-2与y轴交于点A,
∴点A(0,-2),
令y=-2,得:-$\frac{1}{2}$x2=-2,
解得:x1=2,x2=-2,
当y=0时,-$\frac{1}{2}$x2=0,
解得:x1=x2=0,
∴点O(0,0),
∴点B(-2,-2),点C(2,-2),
∴S△BOC=$\frac{1}{2}×4×2=4$.
故答案为:4.
点评 本题主要考查抛物线与x轴的交点,熟记相关的公式,与x轴相交即y=0,是解决此题的关键.

练习册系列答案
相关题目
6.截止到2015年6月底,济南机动车总保有量为1640000辆,用科学记数法表示这个数为( )
| A. | 16.4×105 | B. | 1.64×105 | C. | 0.164×107 | D. | 1.64×106 |
7.已知一个立体图形的三视图如图所示,那么它是( )
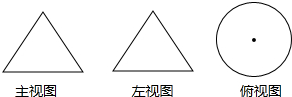

| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 棱柱 |
4.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 2,3,$\sqrt{6}$ | C. | 5,12,13 | D. | $\frac{5}{4}$,1,$\frac{3}{4}$ |
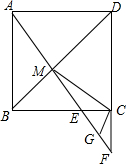 如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证:
如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证: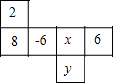 一个正方体的相对的面上所标的两个数,都是互为相反数的两个数,如图是这个正方体的展开图,那么x+y的值为-10.
一个正方体的相对的面上所标的两个数,都是互为相反数的两个数,如图是这个正方体的展开图,那么x+y的值为-10.