题目内容
10. 已知:如图,FA⊥AC,EB⊥AC,垂足分别为A、B,且∠BED+∠D=180°,求证:AF∥CD.
已知:如图,FA⊥AC,EB⊥AC,垂足分别为A、B,且∠BED+∠D=180°,求证:AF∥CD.
分析 在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行,依此可证AF∥EB;同旁内角互补,两直线平行,依此可证BC∥EB;两条直线都和第三条直线平行,那么这两条直线平行,依此可证AF∥CD.
解答 证明:∵FA⊥AC,EB⊥AC,
∴AF∥EB,
∵∠BED+∠D=180°,
∴BC∥EB,
∴AF∥CD.
点评 考查了平行线的判定,关键是熟悉:
(1)定理1:两条直线被第三条所截,如果同位角相等,那么这两条直线平行. 简单说成:同位角相等,两直线平行. (2)定理2:两条直线被第三条所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行. (3 )定理3:两条直线被第三条所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行.(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.若等腰三角形的底角为40°,则它的顶角度数为( )
| A. | 40° | B. | 100° | C. | 80° | D. | 70° |
 如图,以四边形ABCD各个顶点为圆心,1cm长为半径画弧,则图中阴影部分面积之和是π cm2(结果保留π).
如图,以四边形ABCD各个顶点为圆心,1cm长为半径画弧,则图中阴影部分面积之和是π cm2(结果保留π).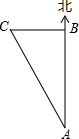 一艘在海上朝正北方向肮行的轮船,从点A到点B航行了240海里时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里后到达点C,此时AC之间的距离为250海里,你能判断船转弯后,是否沿正西方向航行?
一艘在海上朝正北方向肮行的轮船,从点A到点B航行了240海里时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里后到达点C,此时AC之间的距离为250海里,你能判断船转弯后,是否沿正西方向航行?