题目内容
8.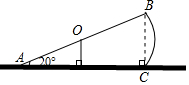 如图,跷跷板AB的一端A碰到地面时,AB与地面的夹角为20°,且
如图,跷跷板AB的一端A碰到地面时,AB与地面的夹角为20°,且OA=OB=2m.
(1)求此时另一端B离地面的距离(即图中垂线段BC的长,精确到0.1m);
(2)跷动AB,使端点B碰到地面,画出点B运动的路线(写出画法,保留画图痕迹),并求出点B运动路线的长.
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
分析 (1)过点B作地面的垂线,垂足为C,在Rt△ABC中,根据正弦函数即可求得;
(2)以点O为圆心,OB长为半径画弧,交地面于点D,则$\widehat{BD}$就是端点B运动的路线;根据弧长公式即可求得.
解答 解:(1)过点B作地面的垂线,垂足为C, 在Rt△ABC中,∠BAC=20°,
在Rt△ABC中,∠BAC=20°,
∴,BC=AB•sin∠BAC=4•sin20°≈4×0.34≈1.4.
答:此时另一端B离地面的距离约为1.4m;
(2)画法:以点O为圆心,OB长为半径画弧,交地面于点D,则$\widehat{BD}$就是端点B运动的路线.
端点B运动路线的长为$\frac{2×20π×2}{180}$=$\frac{4π}{9}$(m).
答:端点B运动路线的长为$\frac{4π}{9}$m.
点评 本题考查了解直角三角形的应用-坡度坡角问题以及弧长的计算.这就要求学生把实际问题转化为直角三角形的问题,利用三角函数解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某中学要组织一次篮球比赛,赛制为单循环形式(毎两队之间都赛一场),计划安排21场比赛,求参加的球队支数,如果设参加的球队支数为x,则可列方程为( )
| A. | $\frac{1}{2}$x(x+1)=21 | B. | x(x+1)=21 | C. | $\frac{1}{2}$x(x-1)=21 | D. | x(x-1)=21 |
16.一份稿件,甲8小时打完,乙6小时打完,则乙的工作效率比甲快百分之几?下面列式正确的是( )
| A. | (8-6)÷8 | B. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{6}$ | C. | $\frac{1}{6}$÷$\frac{1}{8}$ | D. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{8}$ |
20.一个长方形的周长为26cm,若这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,设这个长方形的长为xcm,可列方程( )
| A. | x+1=(26-x)-2 | B. | x+1=(13-x)-2 | C. | x-1=(26-x)+2 | D. | x-1=(13-x)+2 |
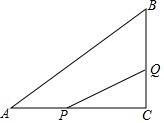 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动 圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是( )
圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是( )


