题目内容
11.大庆市移动通讯公司开设了两种通讯业务:“全球通”使用者先缴50元/月基础 费,然后每通话1分钟,再付0.4元;“神州行”不缴月基础费,每通话1分钟,付话费0.6元(这里均指市内通话).若一个月内通话时间为x分钟,两种通讯方式的费用分别为y1元和y2元.(1)写出y1、y2与x的关系式.
(2)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
分析 (1)根据题意可得“全球通”使用者的费用=50元/月+0.4元×通话时间;“神州行”的费用=0.6元×通话时间,进而可得解析式;
(2)此题要分三种情况:①y1=y2 时,②y1>y2 时,③y1<y2 时,分别列出方程或不等式,再解即可.
解答 解:(1)由题意可知y1=50+0.4x,
y2=0.6x,
(2)当y1=y2 时,即50+0.4x=0.6x,解得x=250,
当y1>y2 时,即50+0.4x>0.6x,解得x<250,
当y1<y2 时,即50+0.4x<0.6x,解得x>250,
∴当用户每月通话时间少于250分钟,选“神州行”,
当多于250分钟选“全球通”,
当通话时间为250分钟时,选择哪种方式都一样.
点评 此题主要考查了一次函数的应用,关键是正确理解题意,找出题目中等量关系,列出函数关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.三角形两边长为4和11,第三边长为3-6m,则m的取值范围是( )
| A. | -2<m<-$\frac{2}{3}$ | B. | m>-2 | C. | -2≤m≤-$\frac{2}{3}$ | D. | m<-2 |
19.某中学要组织一次篮球比赛,赛制为单循环形式(毎两队之间都赛一场),计划安排21场比赛,求参加的球队支数,如果设参加的球队支数为x,则可列方程为( )
| A. | $\frac{1}{2}$x(x+1)=21 | B. | x(x+1)=21 | C. | $\frac{1}{2}$x(x-1)=21 | D. | x(x-1)=21 |
16.一份稿件,甲8小时打完,乙6小时打完,则乙的工作效率比甲快百分之几?下面列式正确的是( )
| A. | (8-6)÷8 | B. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{6}$ | C. | $\frac{1}{6}$÷$\frac{1}{8}$ | D. | ($\frac{1}{6}$-$\frac{1}{8}$)÷$\frac{1}{8}$ |
20.一个长方形的周长为26cm,若这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,设这个长方形的长为xcm,可列方程( )
| A. | x+1=(26-x)-2 | B. | x+1=(13-x)-2 | C. | x-1=(26-x)+2 | D. | x-1=(13-x)+2 |
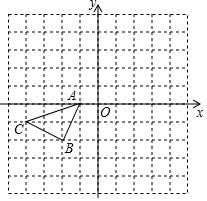 在直角坐标系中,△ABC的三个顶点的位置如图所示:
在直角坐标系中,△ABC的三个顶点的位置如图所示: 如图所示,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是②或③或④.
如图所示,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是②或③或④.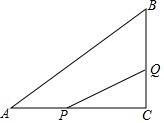 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动