题目内容
2．直线外一点距离此直线3cm，以该点为顶点作等腰直角三角形，使另两顶点在该直线上，这样的等腰直角三角形的面积是（ ）| A． | 3cm2，4.5cm2，9cm2 | B． | 4.5cm2，9cm2 | ||
| C． | 3cm2，9cm2 | D． | 3cm2，4.5cm2 |
分析 由于直线外的一点没有说明是否为直角顶点，故需要分情况讨论．
解答 解：当直线外的一点是等腰直角三角形的顶点时，
由题意可知：AD=3，
∴BD=CD=3，
∴△ABC的面积为：$\frac{1}{2}$×6×3=9cm2，
当直线外的一点不是等腰直角三角形的顶点时，
由题意可知：AC=3，
∴BC=AC=3，
∴△ABC的面积为：$\frac{1}{2}$×3×3=4.5cm2，
故选（B）
点评 本题考查等腰三角形的性质，解题的关键是将直线外的一点进行分类讨论，本题属于中等题型．
练习册系列答案
相关题目
12．用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点称为格点，以格点为顶点的多边形称为格点多边形．设格点多边形的面积为S，该多边形各边上的格点个数之和为m，内部的格点个数为n，试探究S与m、n之间的关系式．
（1）根据图中提供的信息填表：
则S=$\frac{1}{2}$m+n-1（用含m、n的代数式表示）
（2）对正三角形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，如图1、2是该正三角形格点中的两个多边形：设格点多边形的面积为S，该多边形各边上的格点个数之和为m，内部的格点个数为n，试探究S与m、n之间的关系式．则S与m、n之间的关系为S=m+2（n-1）（用含m、n的代数式表示）．
（1）根据图中提供的信息填表：
| 格点多边形各边上的 格点的个数 | 格点边多边形内部的 格点个数 | 格点多边形的面积 | |
| 多边形1 | 4 | 1 | 2 |
| 多边形2 | 5 | 2 | ②$\frac{7}{2}$ |
| 多边形3 | 6 | 3 | 5 |
| 多边形4 | ①5 | 4 | $\frac{11}{2}$ |
| 一般格点多边形 | m | n | S |
（2）对正三角形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，如图1、2是该正三角形格点中的两个多边形：设格点多边形的面积为S，该多边形各边上的格点个数之和为m，内部的格点个数为n，试探究S与m、n之间的关系式．则S与m、n之间的关系为S=m+2（n-1）（用含m、n的代数式表示）．
13．非等边三角形的三条边都是方程x2-6x+8=0的解，则这个三角形的周长是（ ）
| A． | 6 | B． | 8 | C． | 10 | D． | 8 或 10 |
10．如图，水平地面上有一面积为30πcm2的灰色扇形OAB，其中OA=6cm，且OA垂直于地面，将这个扇形向右滚动（无滑动）至点B刚好接触地面为止，则在这个滚动过程中，点O移动的距离是（ ）
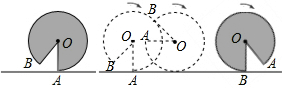
| A． | 10πcm | B． | 20πcm | C． | 24πcm | D． | 30πcm |
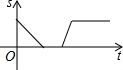
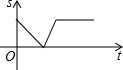
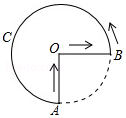诸暨影视城里有一座圆形的土楼，如图，小王从南门点A沿AO匀速直达土楼中心古井点O处，停留拍照后，从点O沿OB也匀速走到点B，紧接着沿$\widehat{BCA}$回到南门，下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是（ ）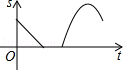
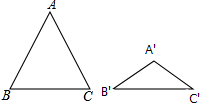如图，△ABC与△A′B′C′都是等腰三角形，且AB=AC=5，A′B′=A′C′=3，若∠B+∠B′=90°，则△ABC与△A′B′C′的面积比为25：9．