题目内容
17.阅读下列材料我们知道,假分数可以化为带分数.例如:$\frac{8}{3}$=$2+\frac{2}{3}$=$2\frac{2}{3}$.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:$\frac{x-1}{x+1}$,$\frac{x^2}{x-1}$这样的分式就是假分式;$\frac{3}{x+1}$,$\frac{2x}{{{x^2}+1}}$这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式和的形式).
例如:$\frac{x-1}{x+1}=\frac{(x+1)-2}{x+1}=\frac{x+1}{x+1}-\frac{2}{x+1}=1-\frac{2}{x+1}$;
$\frac{x^2}{x-1}=\frac{{{x^2}-1+1}}{x-1}=\frac{(x+1)(x-1)+1}{x-1}=x+1+\frac{1}{x-1}$.
(1)分式$\frac{2}{x}$是真分式(填“真分式”或“假分式”);
(2)将分式$\frac{x-1}{x+2}$化为带分式;
(3)若分式$\frac{2x-1}{x+1}$的值为整数,求x的整数值.
分析 (1)根据真分式的定义求解;
(2)利用题中的方法把分子变形为2(x+2)-3,然后写成带分式即可;
(3)先把分式化为带分式,然后利用有理数的整除性求解.
解答 解:(1)分式$\frac{2}{x}$是 真分式;
故答案为真;
(2)$\frac{x-1}{x+2}=\frac{(x+2)-3}{x+2}=1-\frac{3}{x+2}$;
(3)$\frac{2x-1}{x+1}=\frac{2(x+1)-3}{x+1}=2-\frac{3}{x+1}$;
当$\frac{2x-1}{x+1}$为整数时,$\frac{3}{x+1}$也为整数
所以x+1可取得的整数值为±1、±3.
所以x的可能整数值为0,-2,2,-4.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
12.下列方程中,没有实数根的是( )
| A. | x2-6x+9=0 | B. | x2-2x+3=0 | C. | x2-x=0 | D. | (x+2)(x-1)=0 |
2.直线外一点距离此直线3cm,以该点为顶点作等腰直角三角形,使另两顶点在该直线上,这样的等腰直角三角形的面积是( )
| A. | 3cm2,4.5cm2,9cm2 | B. | 4.5cm2,9cm2 | ||
| C. | 3cm2,9cm2 | D. | 3cm2,4.5cm2 |
 如图,四边形ABCD中,∠A=90°,AB=$5\sqrt{3}$,BC=8,CD=6,AD=5.
如图,四边形ABCD中,∠A=90°,AB=$5\sqrt{3}$,BC=8,CD=6,AD=5.
 作图:A,B两村庄要建一个加油站,要求到A,B两村距离相等,且到公路a,b的距离也相等,请你帮忙确定加油站的位置P.(用直尺、圆规作图,保留作图痕迹)
作图:A,B两村庄要建一个加油站,要求到A,B两村距离相等,且到公路a,b的距离也相等,请你帮忙确定加油站的位置P.(用直尺、圆规作图,保留作图痕迹)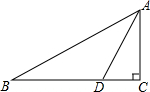 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DC=1,BD=2.求∠B的度数和AC的长.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DC=1,BD=2.求∠B的度数和AC的长.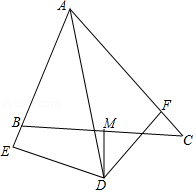 如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论:
如图,△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于D,DE⊥AB交AB的延长线于E,DF⊥AC于F,现有下列结论: